Дипломная работа: Разработка системы управления многосвязных систем автоматического регулирования исполнительного уровня
Введение
Неуклонный рост материальных
и духовных потребностей общества стимулирует развитие всех видов науки, техники
и промышленных технологий. В результате этого происходит модернизация старых и
создание новых технических средств и систем различного целевого назначения. От
устаревших их отличают улучшенные потребительские и эксплуатационно-технические
характеристики (производительность, точность, сложность функций и качество их
исполнения, энергопотребление, надежность, конструктивная сложность, число
элементов, интенсивность и скорость протекания процессов, возможность работы в
пограничных и критических режимах). Сферы их применения разнообразны:
энергетика, транспорт, промышленное производство, авиационная, ракетно-космическая,
военная, медицинская, научная и испытательная техника и др.
Сложные технические
объекты не могут самостоятельно и нормально функционировать (выполнять алгоритм
функционирования) без принудительных (управляющих) воздействий со стороны
специально организованного комплекса средств, образующих управляющую подсистему.
Для реализации основных ее функций, таких как: а) сбор осведомительной информации
о состоянии управляемого объекта и внешней среды; б) преобразование информации
(принятие решения); в) формирование управляющих воздействий (исполнение решения)
применяются специальные технические средства (устройства). При этом суть и цель
автоматизации управления состоит в возможно более полном освобождении человека
от выполнения названных выше функций управляющей подсистемы.
Переход от локальной
автоматизации к комплексной приводит к необходимости одновременного изменения
нескольких управляемых переменных. Усложнение функций, возложенных на
технические объекты, повышение требований к качеству их выполнения;
необходимость учета взаимодействий локальных процессов; повышение порядка и
сложности математических моделей и др. существенно усложняют задачу управления.
При этом сложные технические объекты должны рассматриваться не только как
многомерные, но и как многосвязные. Примерами могут служить летательные
аппараты, их силовые и энергетические установки; исполнительные подсистемы
роботов и т.п. В них многосвязность проявляется в наличии перекрестных связей,
за счет которых управляющее воздействие, поданное на любой из входов, приводит
к изменению несколько выходов.
Сложность алгоритмов
функционирования и математических моделей современных технических объектов, их
многосвязность приводят, как правило, к невозможности применения централизованного
(радиального) управления на основе единой цели и алгоритма,
обеспечивающего наилучшее (или допустимое) значение показателя эффективности.
Это связано с наличием ряда проблем информационного, математического,
методологического и технического характера.
Более конструктивным (при
современном уровне развития науки и техники) является подход децентрализации,
при котором функции управления распределяются между несколькими,
взаимодействующими между собой и с техническим объектом, управляющими центрами
(узлами, устройствами). Организационная структура управляющей подсистемы при
этом усложняется и часто оказывается многоуровневой (иерархической), в
которой между некоторыми парами узлов управления присутствуют отношения соподчинения.
Несмотря на некоторое снижение эффективности по сравнению с гипотетическим
вариантом радиального управления, децентрализация дает возможность практического
осуществления управления сложными техническими объектами. При этом центры
управления верхних (командных) уровней, реализуя более сложные алгоритмы
управления, получают осведомительную информацию от узлов управления
нижних уровней в некотором обобщенном (усредненном) виде. По этой причине
скорости протекания процессов управления на двух соседних уровнях в большинстве
случаев могут различаться в десятки раз. Наиболее быстрыми и оперативными
будут процессы на самом нижнем, исполнительном уровне, где требуемая скорость
изменения управляющих воздействий определяется свойствами управляемого объекта.
Цели (задачи) для узлов управления исполнительного уровня, как правило,
простейшие: регулирование значений управляемых переменных технического объекта
в соответствии с предписанными (со стороны верхних уровней) законами их
изменения во времени. При этом управляющие центры верхних уровней решают более
сложные задачи, связанные с координацией, адаптацией подчиненных им подсистем нижних
уровней и с оптимизацией режимов работы объекта. Определение числа уровней, а
также необходимого числа узлов (центров) управления на каждом уровне в составе
управляющей подсистемы, распределение между ними целей управления, определение
алгоритмов их достижения – вот характерные проблемы, возникающие при разработке
системы с децентрализованным (распределенным) управлением. Для выбора
подходящего варианта организационной структуры управляющей подсистемы в
настоящее время нет аналитических методов, потому используют экспертные оценки,
опыт предыдущих и аналогичных разработок, рекомендации методов структурного
анализа и синтеза сложных систем, методы компьютерного моделирования.
Темпы и скорости
процессов управления на разных уровнях существенно различаются. По степени
оперативности (по частоте принятия решений), по сложности и общности целей
управления, кроме первого (самого нижнего, исполнительного) уровня,
осуществляющего оперативное управление подсистемами технического
объекта, можно укрупнено выделить ещё два более высоких уровня управления:
второй (тактический) уровень и третий (стратегический) уровень.
Каждый из них, в общем случае, может содержать несколько подуровней управления.
Тактический уровень управления осуществляет
согласование, координацию сепаратных подсистем первого уровня, а при
необходимости, обеспечивает им свойства адаптации за счет изменения параметров
их алгоритмов управления.
На стратегическом уровне
осуществляется оптимизация некоторых обобщенных показателей функционирования
сложного технического объекта.
Алгоритмы управления,
реализуемые каждым из уровней, базируются на использовании осведомительной
информации, получаемой от нижестоящих уровней. В то же время функционирование
центра управления любого уровня определяется директивной, управляющей
информацией, поступающей со стороны вышестоящих уровней. Многоуровневый подход
к организации управляющей подсистемы создает предпосылки для разбиения процесса
проектирования системы управления сложными объектами на ряд последовательных
этапов. При этом при разработке алгоритма управления для некоторого уровня
обычно возможна идеализация нижних уровней, при которой считают, что их цели
управления достигаются быстро и точно, а управляющие (директивные) воздействия
со стороны верхнего уровня «замораживаются», либо имеют некоторый типовой вид.
Сложные (многосвязные)
технические объекты в совокупности с узлами (устройствами) управления первого,
исполнительного уровня образуют подсистемы оперативного управления, которые
представляют собой многосвязные системы автоматического регулирования (МСАР)
по типу следящих систем. Задающие воздействия для них формируются на втором, тактическом
уровне, а цели управления состоят в воспроизведении с достаточной точностью
требуемых законов изменения для каждой управляемой переменной. При этом
критерием оценки эффективности МСАР будут функционалы от ошибок воспроизведения
задающих воздействий. На этапе расчета МСАР эти воздействия принимаются
типовыми, а преобразовательные и собственные динамические свойства МСАР определенным
образом ограничиваются, чтобы при синтезе алгоритмов управления тактического
уровня их неидеальностью можно было пренебречь.
Проектирование МСАР
следящего типа, как подсистем исполнительного уровня в составе многоуровневой
системы управления представляет собой традиционную для ТАУ задачу динамического
синтеза. Однако ее решение имеет весьма существенные особенности,
обусловленные факторами многомерности и многосвязности объекта управления ОУ;
высоким порядком его математической модели; особенностями оценки качества
работы МСАР и др. По этим причинам непосредственное применение традиционных инженерных
методов синтеза одномерных следящих СУ оказываются невозможным без их обобщения
на многомерный случай. Научные работы в этой области, в основном, посвящены
аналитическим методам оптимального синтеза МСАР. Используемые при этом
функционалы качества (критерии оптимальности) назначаются, как правило, исходя
из условий математической разрешимости задачи, и в большинстве своем имеют
обобщенный, абстрактный характер, слабо связанный с инженерными приложениям и
требованиями.
Несмотря на большое число
публикаций и монографий, в основном двадцатилетней давности, в учебной
литературе по теории автоматического управления инженерным методам
динамического синтеза МСАР не уделяется должного внимания. Именно этим
обусловлен выбор темы исследования.
Цель работы: частичный синтез и исследование многомерной САР исполнительного
уровня в составе распределенной системы управления сложным техническим объектом.
Исходные данные. Структурная схема рассматриваемой МСАР, показана на
рисунке 1.
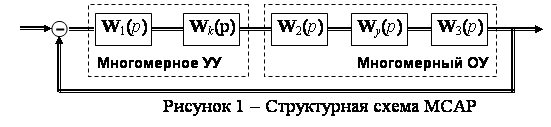
Передаточные матрицы (ПМ) линейных
МДЗ в составе двумерной МСАР имеют вид:
W1(p)=diag{Wp1(p); Wp2(p)};
W2(p)=diag{W01(p); W02(p)};
W3(p)=diag
(1/p); 1/p)},
где Wpi(p) – подлежащая определению ПФ i-го
сепаратного регулятора; i = 1; 2.
W0i(p) = 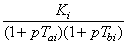 – ПФ неизменяемой части i-го
сепаратного канала;
– ПФ неизменяемой части i-го
сепаратного канала;
Wk(p) – ПМ компенсатора (в работе рассматриваются
два его варианта):
a) Wk(p) = [E+Wx(p)] – ПМ компенсатора с прямыми перекрестными
связями;
b) Wk(p) = [E – Wx(p)]–1 – ПМ компенсатора с обратными перекрестными связями.
Здесь 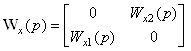 ,
а Wx1(p) и Wx2(p) – подлежащие
определению передаточные функции прямых (или обратных) перекрестных связей
в составе последовательного компенсатора, обеспечивающего
свойство автономности каналов регулирования.
,
а Wx1(p) и Wx2(p) – подлежащие
определению передаточные функции прямых (или обратных) перекрестных связей
в составе последовательного компенсатора, обеспечивающего
свойство автономности каналов регулирования.
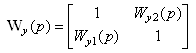 , где
, где 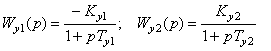 –
ПФ перекрестных связей в объекте управления ОУ, а Ky1=15; Ky2=10; Ty1=0.4Ta1; Ty2=1.5Tb2.
–
ПФ перекрестных связей в объекте управления ОУ, а Ky1=15; Ky2=10; Ty1=0.4Ta1; Ty2=1.5Tb2.
Таблица 1 – Исходные данные
|
№ вар.
|
i
|
Кi, с-1
|
Tai, с
|
Tbi, с
|
wсрi
|
Mi
|
Схема
ЦСАР
|
| 6 |
1 |
125 |
0.07 |
0.01 |
41 |
1.23 |
a) |
| 2 |
135 |
0.11 |
0.009 |
33 |
1.35 |
1. Синтез и исследование непрерывной
МСАР
1.1
Определение ПФ сепаратных регуляторов
Изобразим структурную схему МСАР
при отсутствии перекрестных связей в многомерном управляющем устройстве и в
многомерном объекте управления (Рисунок 1.1)

Рисунок 1.1 – Структурная схема
МСАР при отсутствии перекрестных связей в МУУ и МОУ
Запишем передаточные матрицы с
заданными числовыми значениями параметров:
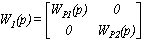 ;
;
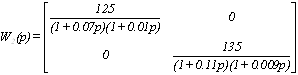 ;
;
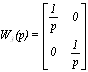 ;
;
Применяя формулы В.А. Бесекерского
для типовой «симметричной» ЛАХ, выберем вид и параметры ПФ Wр1(p) и Wр2(p),
обеспечивающие заданные свойства сепаратным каналам по точности (коэффициент
добротности K=Ki), по быстродействию (wср) и по колебательности (M).
1) Первый сепаратный канал
Изобразим структурную схему
первого сепаратного канала (Рисунок 1.2)

Рисунок 1.2 – Структурная схема
первого сепаратного канала
Запишем передаточную функцию
первого разомкнутого сепаратного канала:
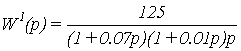 ; (1.1)
; (1.1)
Определим, обеспечиваются ли
заданные в ТЗ свойства сепаратного канала.
Построим ЛАЧХ первого сепаратного
канала. Построение проведем на масштабно-координатной бумаге.
Первая асимптота ЛАЧХ с наклоном -20
дБ/дек пересекает ось L(w) в точке 20logK1, что соответствует
требованию ТЗ по точности.
Определим частоту среза.
log wср=1.6, wcp=40 рад/с. Она близка
к требуемому значению.
Построим АЧХ замкнутого
сепаратного канала (Рисунок 1.3), как зависимость модуля частотной передаточной
функции замкнутого канала от частоты.
Передаточная функция замкнутого
канала определяется формулой
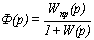 (1.2)
(1.2)
Определим показатель
колебательности М, используя формулу
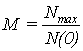 ; (1.3)
; (1.3)
где N(w) – модуль частотной передаточной функции замкнутого канала.
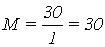
Свойства первого сепаратного
канала по колебательности не соответствуют заданным в ТЗ.
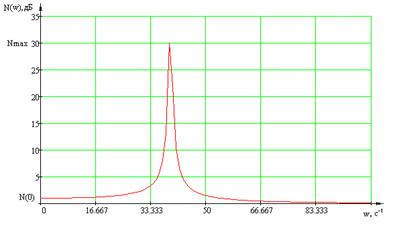
Рисунок 1.3 – АЧХ замкнутого
сепаратного канала 1
Определим передаточную функцию
сепаратного регулятора.
Типовая «симметричная» ЛАХ на
среднечастотном участке имеет наклоны (-40 дБ/дек; -20 дБ/дек; -40 дБ/дек).
Сравнивая с заданной передаточной функцией первого сепаратного канала,
определим, что желаемая передаточная функция будет иметь вид:
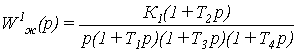 . (1.4)
. (1.4)
Для оценки параметров желаемой
передаточной функции воспользуемся формулами Бесекерского:
 (1.5)
(1.5)
Проведем построение желаемой ЛАЧХ
на масштабно-координатной бумаге (Приложение 1а), из построения определим
постоянную времени Т1 и ЛАЧХ сепаратного регулятора.
Таким образом, передаточная
функция первого сепаратного регулятора, обеспечивающая заданные в ТЗ свойства
первому сепаратному каналу, имеет вид:
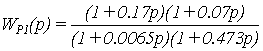 .
.
Передаточная функция разомкнутого
сепаратного канала:
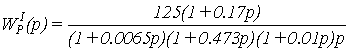 . (1.6)
. (1.6)
Определим показатель
колебательности скорректированного сепаратного канала по формуле (1.3), для
этого построим АЧХ замкнутого сепаратного канала. (Рисунок 1.4)
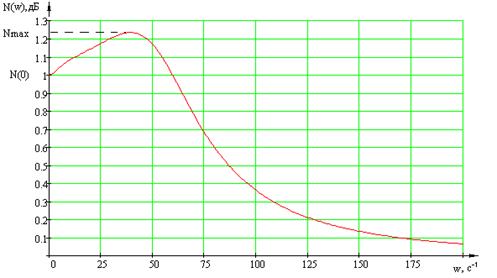
Рисунок 1.4 – АЧХ замкнутого
сепаратного канала 1 с регулятором
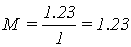 .
.
Свойства сепаратного канала по
точности, быстродействию и колебательности соответствуют заданным в ТЗ.
2) Второй сепаратный канал
Изобразим структурную схему
второго сепаратного канала (Рисунок 1.5)

Рисунок 1.5 – Структурная схема
второго сепаратного канала
Запишем передаточную функцию
второго разомкнутого сепаратного канала:
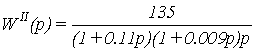 ; (1.7)
; (1.7)
Определим, обеспечиваются ли
заданные в ТЗ свойства сепаратного канала.
Построим ЛАЧХ вотрого сепаратного
канала. Построение проведем на масштабно-координатной бумаге (Приложение 1б).
Первая асимптота ЛАЧХ с наклоном -20
дБ/дек пересекает ось L(w) в точке 20logK2, что соответствует
требованию ТЗ по точности.
Определим частоту среза.
log wср=1.53, wcp=34 рад/с. Она близка
к требуемому значению.
Построим АЧХ замкнутого
сепаратного канала (Рисунок 1.6), определим показатель колебательности М,
используя формулу (1.3)
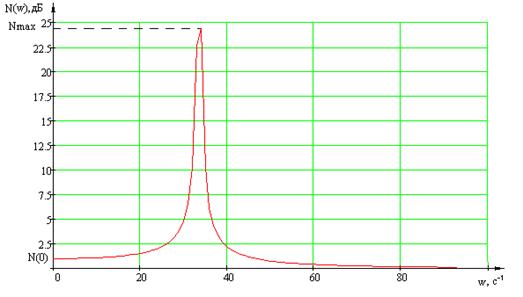
Рисунок 1.6 – АЧХ замкнутого
сепаратного канала 2
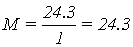
Свойства второго сепаратного
канала по колебательности не соответствуют заданным в ТЗ.
Определим передаточную функцию второго
сепаратного регулятора.
Аналогично первому сепаратному
каналу, желаемая передаточная функция будет иметь вид:
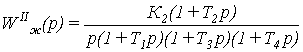 . (1.8)
. (1.8)
Для оценки параметров желаемой
передаточной функции воспользуемся формулами Бесекерского (1.4).
Проведем построение желаемой ЛАЧХ
на масштабно-координатной бумаге (Приложение 1б), из построения определим
постоянную времени Т1 и ЛАЧХ сепаратного регулятора.
Таким образом, передаточная
функция второго сепаратного регулятора, обеспечивающая заданные в ТЗ свойства второму
сепаратному каналу, имеет вид:
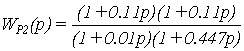 .
.
Передаточная функция разомкнутого
сепаратного канала:
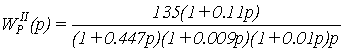 (1.9)
(1.9)
Определим показатель
колебательности скорректированного сепаратного канала по формуле (1.2), для
этого построим АЧХ замкнутого сепаратного канала. (Рисунок 1.7)
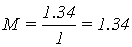 .
.
Свойства сепаратного канала по
точности, быстродействию и колебательности соответствуют заданным в ТЗ.
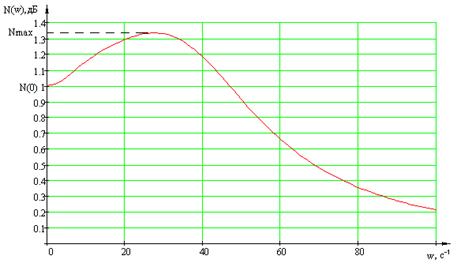
Рисунок 1.7 – АЧХ замкнутого
сепаратного канала 2 с регулятором
1.2
Исследование свойств сепаратных каналов МСАР
Прямые и частотные показатели качества
переходного процесса
Для определения прямых показателей
качества переходного процесса получим переходные характеристики первого и
второго сепаратных каналов с помощью программного пакета MATLAB
(Приложение 2)
1) Первый сепаратный канал
Переходная характеристика для первого
сепаратного канала изображена на рисунке 1.8.
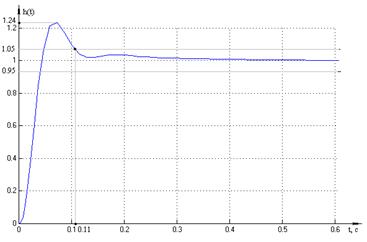
Рисунок 1.8 – Переходная
характеристика первого сепаратного канала
Используя график переходной
характеристики определим время переходного процесса как время, по истечении
которого отклонение управляемой величины от установившегося значения станет
менее 5%.
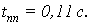
Определим перерегулирование как
отношение максимального отклонения управляемой величины от своего
установившегося значения к установившемуся значению.
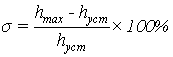 (1.10)
(1.10)
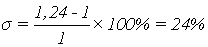
Частотный показатель качества
переходного процесса – показатель колебательности – был определен в п. 1.1
в рамках проверки свойств сепаратного канала.
2) Второй сепаратный канал
Переходная характеристика для
второго сепаратного канала изображена на рисунке 1.9.
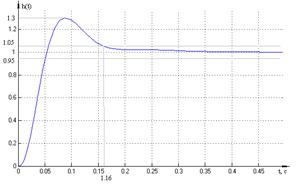
Рисунок 1.9 – Переходная
характеристика второго сепаратного канала
Аналогично первому сепаратному
каналу:
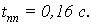
Определим перерегулирование по
формуле (1.10)
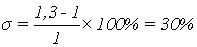
Частотный показатель качества
переходного процесса – показатель колебательности – был определен в п. 1.1
в рамках проверки свойств сепаратного канала.
Определим показатели точности в
виде амплитудных (δА) и фазовых (δφ) искажений
на частоте w1=0,3wср2
Частота среза второго сепаратного
канала определена техническим заданием.
wср2=33 рад/с,
w1=0,3∙33=9,9
рад/с.
Найдем амплитудно-фазовые
искажения для каждого сепаратного канала по формулам:
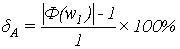 (1.11)
(1.11)
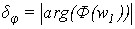 (1.12)
(1.12)
где
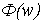 – частотная передаточная функция замкнутого сепаратного
канала.
– частотная передаточная функция замкнутого сепаратного
канала.
1) Первый сепаратный канал
Запишем частотную передаточную
функцию замкнутого канала, используя формулу (1.2):
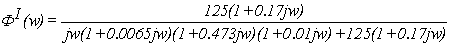 (1.13)
(1.13)
Определим амплитудные искажения:
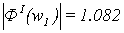
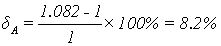
Определим фазовые искажения:
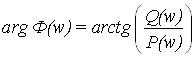 ,
,
где Q(w) и P(w) – мнимая и
действительная часть частотной передаточной функции замкнутого канала.
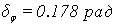
2) Второй сепаратный канал
Запишем частотную передаточную
функцию замкнутого канала:
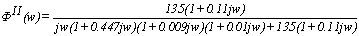 . (1.14)
. (1.14)
Определим амплитудные искажения:
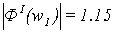
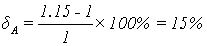
Определим фазовые искажения:
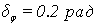
Определим запасы устойчивости
сепаратных каналов, используя критерий Найквиста на плоскости ЛЧХ.
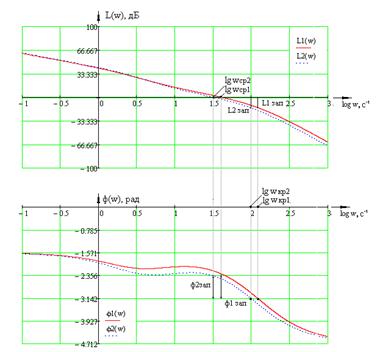
Построим ЛЧХ разомкнутых
сепаратных каналов. (Рисунок 1.10)
По графикам определим запасы
устойчивости
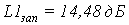
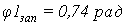
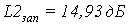
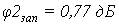
1.3 Исследование свойств исходной МСАР (при Wk(p)=E)
Изобразим структурную схему МСАР с
учетом перекрестных связей в многомерном объекте управления (Рисунок 1.11)

Рисунок 1.11 – Структурная схема
МСАР с учетом перекрестных связей в МОУ
Передаточная матрица 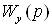 имеет следующий вид:
имеет следующий вид:
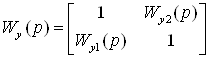 ,
,
где 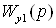 ,
,
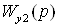 – передаточные функции
перекрестных связей в объекте управления
– передаточные функции
перекрестных связей в объекте управления
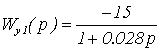 ,
,
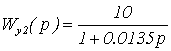 .
.
1) Обобщенный критерий Найквиста
Запишем передаточную матрицу
разомкнутой системы, изображенной на рисунке 1.10
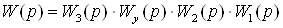 (1.15)
(1.15)
Выражение для получения
характеристического уравнения:
det [E+W(p)] = 0. (1.16)
Здесь [E+W(p)] – матрица
возвратных разностей. Ее определитель представляет собой дробно-рациональную
функцию H(p), в числителе которой – характеристический полином jз(p) для замкнутой МСАР, а в знаменателе – характеристический
полином jр(p) для разомкнутой
МСАР:
H(p) = jз(p)/jр(p). (1.17)
Эта особенность функции H(p)
используется для получения обобщенного критерия Найквиста при
исследовании устойчивости замкнутой МСАР.
С помощью программного пакета
MathCAD найдем характеристический полином разомкнутой МСАР (Приложение 3а).
Приравняем полученный полином к нулю и получим корни характеристического
уравнения разомкнутой МСАР:
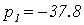 ,
, 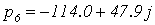
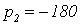 ,
, 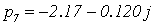
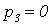 ,
, 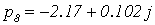
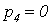 ,
, 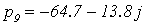
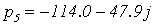 ,
, 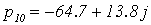
Разомкнутая МСАР находится на
апериодической границе устойчивости.
Построим обобщенный годограф
Найквиста. Произведем замену 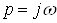 и
представим определитель матрицы возвратных разностей в виде суммы действительной
и мнимой части:
и
представим определитель матрицы возвратных разностей в виде суммы действительной
и мнимой части:
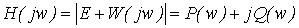
Построим обобщенный годограф
Найквиста (рисунок 1.12) с помощью программного пакета MathCAD (Приложение 3б).
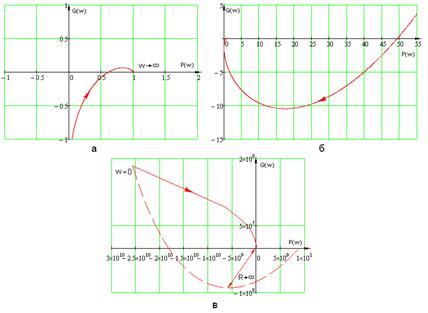
Рисунок 1.12 – Обобщенный годограф
Найквиста
а) годограф на высокочастотном
участке
б) годограф на среднечастотном
участке
в) общий вид годографа
Если разомкнутая система находится
на апериодической границе устойчивости, то для устойчивости замкнутой МСАР
необходимо и достаточно, чтобы обобщенный годограф Найквиста, дополненный на
участке разрыва дугой бесконечно большого радиуса, не охватывал точку с координатами
(0; j0).
Так как обобщенный годограф
Найквиста, дополненный на участке разрыва дугой бесконечно большого радиуса,
охватывает точку с координатами (0; j0) (рисунок 1.12 в),
то замкнутая МСАР является неустойчивой.
2) Метод эквивалентирования
относительно первого канала
Рассмотрим детализирванную до
уровня одномерных звеньев структурную схему МСАР (Рисунок 1.13)
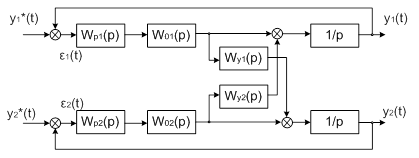
Рисунок 1.13 – Детализирванная до
уровня одномерных звеньев структурная схема МСАР
Изобразим структурною схему с
учетом только внешнего воздействия первого канала регулирования, тогда второй
канал регулирования представим эквивалентным звеном (Рисунок 1.14).
Определим передаточную функцию
эквивалентного звена:
 (1.18)
(1.18)
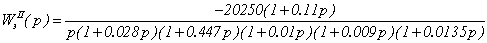
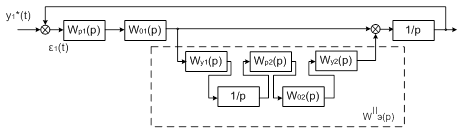
Рисунок 1.14 – Структурная схема с
эквивалентным второму каналу регулирования звеном
Запишем передаточную функцию
разомкнутой системы
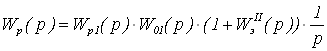 (1.19)
(1.19)
Для устойчивости системы
необходимо и достаточно, чтобы все корнии ее характеристического уравнения были
левыми.
Запишем характеристическое
уравнение замкнутой системы:
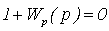
С помощью программного пакета MathCad найдем
его корни (Приложение 4)
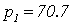 ,
, 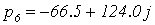
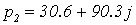 ,
, 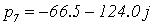
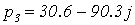 ,
, 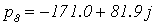
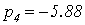 ,
, 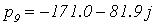
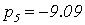 ,
, 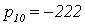
Не все корни характеристического уравнения
замкнутой системы левые, следовательно, система неустойчива.
С помощью обобщенного годографа Найквиста
подберем такую пару значений параметров К1 и К2,
при которых МСАР находится на колебательной границе устойчивости.
Значения параметров 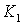 и
и 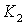 , при которых МСАР
находится на колебательной границе устойчивости, следующие:
, при которых МСАР
находится на колебательной границе устойчивости, следующие:
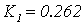 ,
,
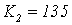 .
.
Изобразим годограф Найквиста
системы с найденными коэффициентами в области высоких частот (Рисунок 1.15).
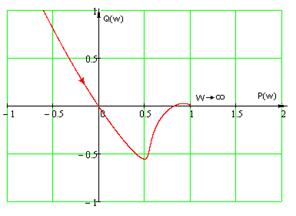
Рисунок 1.15 – Обобщенный годограф
Найквиста при 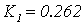 ,
, 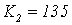
Проверим правильность найденных
значений моделированием МСАР (Приложение 5). Графики переходных процессов,
полученные в результате моделирования, представим на рисунке 1.16.
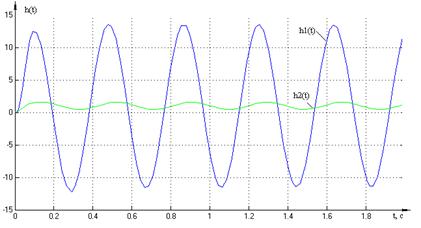
Рисунок 1.16 – Переходные
характеристики
Графики переходных характеристик
представляют собой незатухающие колебания, следовательно, при заданных
параметрах система находится на границе устойчивости.
Запишем передаточную матрицу
замкнутой системы, изображенной на рисунке 1.10.
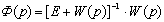 ,
,
где W(p) – передаточная матрица разомкнутой системы (1.15),
определенная в пункте 1.3.1.
Рассматриваемая система имеет два
входа и два выхода, следовательно, передаточная матрица замкнутой системы имеет
вид:
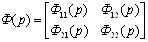 . (1.20)
. (1.20)
Передаточная матрица замкнутой
системы, соответствующая паре «вх. 1 – вых. 1», – 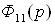 , паре «вх. 1
– вых. 2», –
, паре «вх. 1
– вых. 2», – 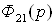 .
.
Построим АЧХ замкнутой МСАР
относительно пар «вх. 1 – вых. 1» и «вх. 1
– вых. 2» с помощью программного пакета MathCAD (Приложение 6а).
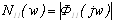 ,
,
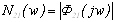 .
.
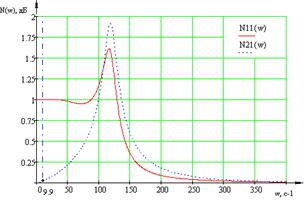
Рисунок 1.17 – АЧХ замкнутой МСАР
относительно пар «вх. 1 – вых. 1» и «вх. 1
– вых. 2»
Определим ординаты построенных
характеристик на частоте 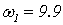
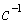 :
:
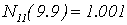 ,
,
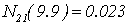 .
.
За точность МСАР в установившемся
режиме отвечает низкочастотный участок АЧХ, по которому можно определить
амплитудно-фазовые искажения.
Проведем сравнение АЧХ первого
сепаратного канала и АЧХ исходной системы относительно пары «вх1-вых1».
Представим их на одном графике.
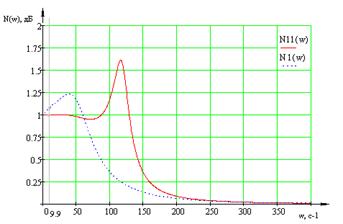
Рисунок 1.18 – АЧХ замкнутой МСАР
относительно пары «вх. 1 – вых. 1» и первого
сепаратного канала
Если предположить, что
установившийся режим существует, то, судя по низкочастотному диапазону АЧХ,
следствием влияния перекрестных связей является уменьшение амплитудных
искажений на рассматриваемой частоте w1=9.9 рад.
Построим графики переходных
функций относительно пар «вх. 1 – вых. 1», «вх.
1 – вых. 2» в программном пакете MathCAD (Приложение 6б) с
использованием ранее записанной передаточной матрицей замкнутой системы (1.20).
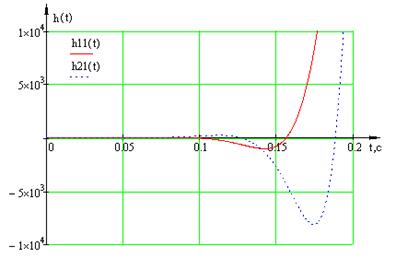
Рисунок 1.19 – Переходных функций
относительно пар «вх. 1 – вых. 1», «вх. 1
– вых. 2»
По графикам переходных функций
видно, что исходная двумерная САР (при 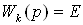 )
является неустойчивой. Таким образом, введенные перекрестные связи в объект
управления ухудшают динамические свойства МСАР.
)
является неустойчивой. Таким образом, введенные перекрестные связи в объект
управления ухудшают динамические свойства МСАР.
1.4 Расчет
последовательного компенсатора (частичный синтез автономной САР)
Изобразим структурную схему МСАР с
последовательным компенсатором (Рисунок 1.20)

Рисунок 1.20 – Структурная схема
МСАР с учетом перекрестных связей в МОУ
Передаточная матрица компенсатора 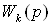 имеет вид
имеет вид
a) 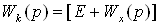 –
для компенсатора с прямыми перекрестными связями;
–
для компенсатора с прямыми перекрестными связями;
b) 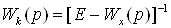 –
для компенсатора с обратными перекрестными связями,
–
для компенсатора с обратными перекрестными связями,
Здесь
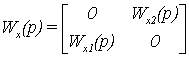 .
.
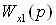 ,
, 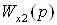 – подлежащие
определению передаточные функции перекрестных связей последовательного
компенсатора.
– подлежащие
определению передаточные функции перекрестных связей последовательного
компенсатора.
Необходимым и достаточным условием
полной автономности каналов регулирования является диагональный вид
передаточной матрицы Ф(p) замкнутой МСАР относительно задающих воздействий:
Фij(p)=0 при i
¹j
или Ф(p) =diag{Фii(p)}.
Для структуры с единичной
отрицательной обратной связью (ЕООС) математические условия автономности можно
получить для передаточной матрицы разомкнутой системы.
В рассматриваемом случае САР
является двумерной, когда число перекрестных связей невелико, их передаточные
функции легко получить на основе принципа двухканальности Б.Н. Петрова.
1) МСАР с прямыми перекрестными
связями в компенсаторе
Рассмотрим детализирванную до
уровня одномерных звеньев структурную схему разомкнутой МСАР (Рисунок 1.21)
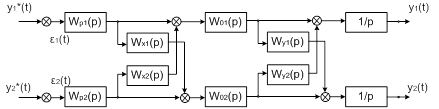
Рисунок 1.21 – Детализирванная до
уровня одномерных звеньев структурная схема разомкнутой МСАР
Передаточную функцию прямой
перекрестной связи Wx1(p) определим из условия равенства нулю суммы передаточных
функций двух каналов распространения сигнала ε1(p) до второго выхода МОУ.
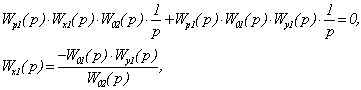
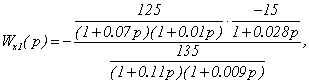
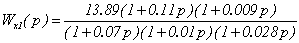 .
.
Аналогично определим и
передаточную функцию Wx2(p):
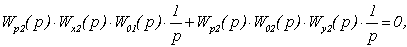
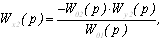
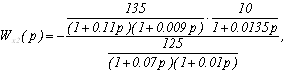
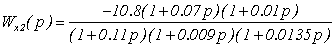 .
.
Динамические свойства автономных
каналов регулирования в общем случае могут отличаться от свойств
соответствующих сепаратных каналов регулирования, получаемых формальным
отбрасыванием всех перекрестных связей и МОУ, и в регуляторе. В случае точного
совпадения этих свойств в МСАР достигается абсолютная автономность, а иначе
обычная, простая автономность.
Определим вид автономности
системы. Для этого сравним передаточные функции разомкнутых автономных и сепаратных
каналов регулирования.
Передаточная функция разомкнутой
системы с учетом перекрестных связей имеет вид:
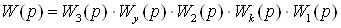 (1.21)
(1.21)
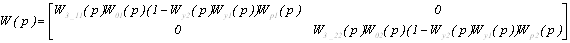
Передаточная
матрица разомкнутой системы без учета перекрестных связей:
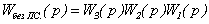
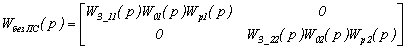
Соответствующие передаточные
функции разомкнутых автономных и сепаратных каналов регулирования не совпадают,
а, следовательно, не совпадают и свойства этих каналов. Значит, наблюдается
простая автономность каналов.
2) МСАР с обратными перекрестными
связями в компенсаторе
Рассмотрим детализирванную до
уровня одномерных звеньев структурную схему разомкнутой МСАР (Рисунок 1.20)
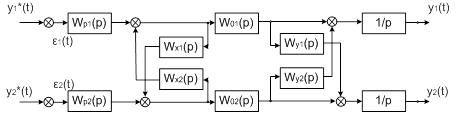
Рисунок 1.20 – Детализирванная до
уровня одномерных звеньев структурная схема разомкнутой МСАР
Передаточную функцию обратной
перекрестной связи Wx1(p) определим из условия равенства нулю суммы передаточных
функций двух каналов распространения сигнала ε1(p) до второго выхода МОУ.
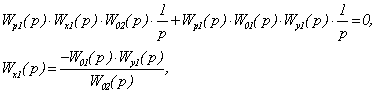
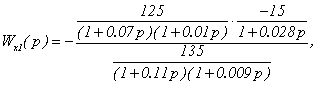
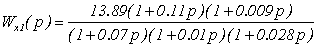 .
.
Аналогично определим и
передаточную функцию Wx2(p):
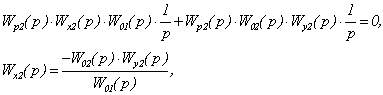
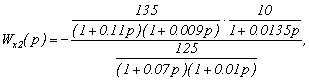
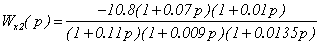 .
.
Определим вид автономности
системы. Для этого сравним передаточные функции разомкнутых автономных и
сепаратных каналов регулирования.
Передаточная функция разомкнутой
системы с учетом перекрестных связей имеет вид:
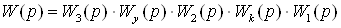 (1.22)
(1.22)
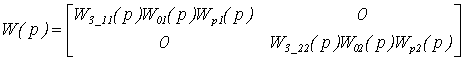
Передаточная
матрица разомкнутой системы без учета перекрестных связей:
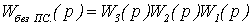
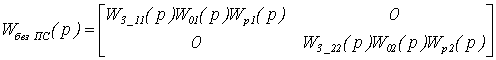
Соответствующие передаточные
функции разомкнутых автономных и сепаратных каналов регулирования совпадают, а,
следовательно, совпадают и свойства этих каналов. Значит, наблюдается
абсолютная автономность каналов.
1) МСАР с прямыми перекрестными
связями в компенсаторе
Запишем передаточную матрицу
замкнутой системы.
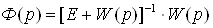 ,
,
где W(p) – передаточная матрица разомкнутой системы (1.21),
определенная в пункте 1.4.1 (1)
Рассматриваемая передаточная
матрица имеет вид:
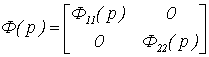 .
.
где 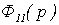 ,
,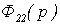 – передаточные функции
замкнутых автономных каналов регулирования.
– передаточные функции
замкнутых автономных каналов регулирования.
Построим АЧХ для каждого из
автономных каналов (Приложение 7а)
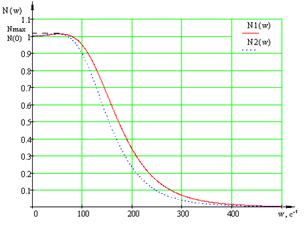
Рисунок 1.21 – АЧХ замкнутых
автономных каналов регулирования
Определим показатель
колебательности по формуле (1.2):
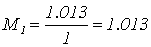
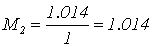
Построим переходные характеристики
(рисунок 1.22) для каждого из автономных каналов регулирования (Приложение 7б).
По графикам переходных функций
видно, что переходный процесс расходится.
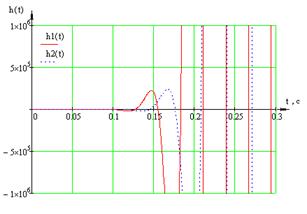
Рисунок 1.22 – Переходные
характеристики автономных каналов регулирования
2) МСАР с обратными перекрестными
связями в компенсаторе
Поскольку в п. 1.4.1
доказано, что при включении последовательного компенсатора с обратными
перекрестными связями наблюдается абсолютная автономность каналов
регулирования, то характеристики автономных каналов регулирования совпадают с
аналогичными характеристиками сепаратных каналов.
Проверим это моделированием МСАР в
программном пакете MATLAB. Получим переходные характеристики автономных каналов МСАР
с обратными перекрестными связями.
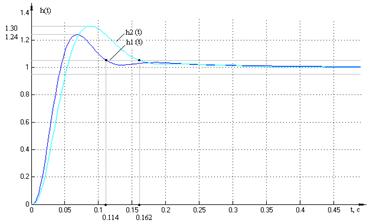
Рисунок 1.23 – Переходные
характеристики автономных каналов регулирования МСАР с обратными ПС
Определим время переходного
процесса и перерегулирования по графикам.
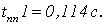
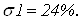
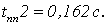
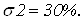
Отметим, что значения прямых
показателей качества переходного процесса автономных каналов МСАР с обратными
перекрестными связями совпадают с аналогичными показателями сепаратных каналов.
Поскольку исходная МСАР
неустойчива, говорить о прямых показателях качества системы некорректно.
Передаточная матрица разомкнутой
системы определена в п. 1.4.1.
Используя передаточные функции
разомкнутых автономных каналов регулирования построим ЛЧХ для каждого из
случаев перекрестных связей и определим запасы устойчивости автономных каналов
регулирования.
1) МСАР с прямыми перекрестными
связями в компенсаторе
С помощью программного пакета MathCad
построим графики ЛЧХ для каждого из разомкнутых каналов регулирования (Приложение
9а).
По графикам ЛЧХ (рисунок 1.24)
видно, что критическая частота меньше частоты среза, следовательно, автономные
каналы регулирования с прямыми перекрестными связями в компенсаторе
неустойчивы, а, следовательно, неустойчива и рассматриваемая МСАР.
Добьемся устойчивости автономных
каналов регулирования.
Рассматриваемые выше сепаратные
каналы устойчивы и удовлетворяют требованиям ТЗ по точности, быстродействию и
колебательности.
Передаточные функции каждого из
сепаратных каналов в общем виде записываются:
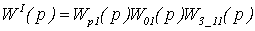 ,
,
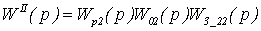 ;
;
Рисунок 1.24 – ЛЧХ автономных
каналов регулирования МСАР с прямыми ПС в компенсаторе
Сравним их с передаточными
функциями автономных каналов регулирования, которые имеют вид:
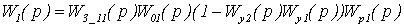
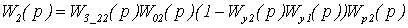
Отметим, что если ввести в цепь
каждого автономного канала такое корректирующее устройство, которое
компенсировало бы множитель 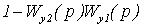 , то
передаточные функции автономных каналов регулирования совпадут с передаточными
функциями сепаратных каналов, будет наблюдаться абсолютная автономность каналов
МСАР и следующее из этого удовлетворение рассматриваемыми каналами требований
ТЗ.
, то
передаточные функции автономных каналов регулирования совпадут с передаточными
функциями сепаратных каналов, будет наблюдаться абсолютная автономность каналов
МСАР и следующее из этого удовлетворение рассматриваемыми каналами требований
ТЗ.
Таким корректирующим устройством
будет включенный последовательно в цепь контур следующего вида:

Представим структурную схему
скорректированной МСАР с прямыми перекрестными связями в компенсаторе.
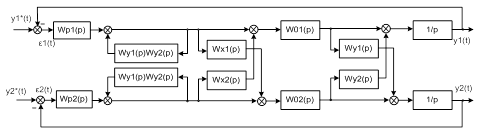
Рисунок 1.25 – Детализированная до
уровня одномерных звеньев структурная схема скорректированной МСАР с прямыми ПС
Построим ЛЧХ автономных каналов
регулирования. (Рисунок 1.26).
Определим запасы устойчивости.
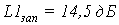
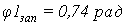
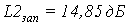
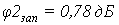
Поскольку введением
корректирующего контура удалось добиться абсолютной автономности системы,
запасы устойчивости автономных каналов регулирования МСАР с прямыми
перекрестными связями совпадают с запасами устойчивости сепаратных каналов
регулирования.
Из устойчивости автономных каналов
регулирования следует устойчивость и рассматриваемой МСАР.
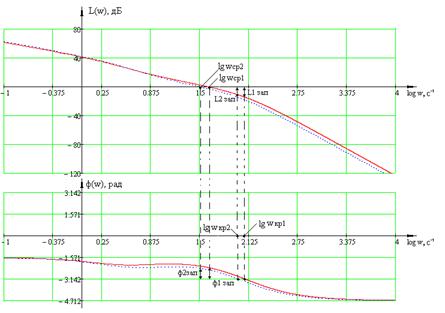
Рисунок 1.26 – – ЛЧХ автономных
каналов регулирования с МСАР с прямыми ПС в компенсаторе
2) МСАР с обратными перекрестными
связями в компенсаторе
С помощью программного пакета MathCad
построим графики ЛЧХ для каждого из разомкнутых каналов регулирования (Приложение
9б).
По графикам ЛЧХ видно, что критическая
частота больше частоты среза, следовательно, автономные каналы регулирования с
обратными перекрестными связями в компенсаторе устойчивы.
Определим запасы устойчивости.
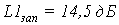
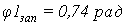
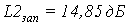
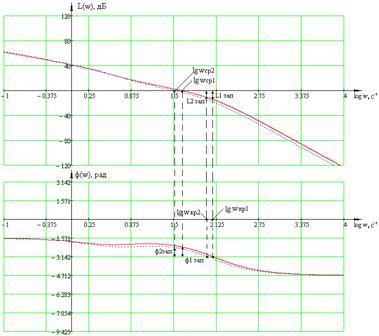
Рисунок 1.24 – ЛЧХ автономных
каналов регулирования
Поскольку в п. 1.4.1
доказано, что при включении последовательного компенсатора с обратными
перекрестными связями наблюдается абсолютная автономность каналов регулирования,
то запасы устойчивости автономных каналов регулирования совпадают с запасами
устойчивости сепаратных каналов.
Из устойчивости автономных каналов
регулирования следует устойчивость и всей рассматриваемой МСАР.
Показатели точности в виде
амплитудных искажений на частоте w1=9.9c-1 для сепаратных
каналов регулирования были определены в п. 1.2.2. Эти величины совпадают с
амплитудными искажениями автономных каналов регулирования МСАР с обратными
перекрестными связями в компенсаторе и прямыми перекрестными связями в
компенсаторе с учетом корректировки, так как в данных случаях наблюдается
абсолютная автономность каналов регулирования.
Амплитудные искажения автономных
каналов регулирования МСАР с прямыми перекрестными связями в компенсаторе без
учета корректировки определим по графику АЧХ для этих каналов, изображенному на
рисунке 1.21.
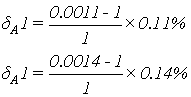
Составим сравнительную таблицу
амплитудных искажений для автономных каналов регулирования и сепаратных каналов
регулирования.
Таблица 1 – Амплитудные искажения
|
|
Сепаратные каналы
|
Автономные каналы
|
|
1 канал
|
2 канал
|
Прямые ПС
|
Прямые ПС
|
|
До корректировки
|
После корректир.
|
|
|
|
1 канал
|
2 канал
|
1 канал
|
2 канал
|
1 канал
|
2 канал
|
|
Амплитудные искажения 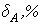
|
8,2 |
15 |
0,11 |
0,14 |
8,2 |
15 |
8,2 |
15 |
Предполагая, что установившийся
режим существует для каждого из вариантов перекрестных связей в компенсаторе,
можно отметить, что прямые перекрестные связи обеспечивают большую точность по
величине амплитудных искажений.
2. Синтез и исследование микропроцессорной МСАР
2.1
Функциональная схема цифровой МСАР. Расчетная структурная схема
Перейдем от непрерывной МСАР к
цифровой. Для этого произведем замену непрерывного корректирующего устройства
на цифровое корректирующее устройство.
Изобразим функциональную схему
цифровой МСАР.
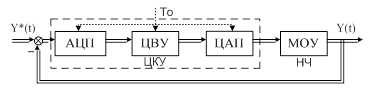
Рисунок 2.1 – Функциональная схема
цифровой МСАР
ЦВУ, АЦП и ЦАП – цифровое
корректирующее устройство (ЦКУ), работающее с периодом 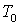 .
.
Структурный метод основан на
замене «нестандартных» элементов, какими являются устройства дискретного
действия, их эквивалентными схемами замещения с последующими структурными
преобразованиями.
Основными этапами структурного
метода при получении расчетных структурных схем являются следующие:
1.
Замещение. Все устройства дискретного
действия в составе исходной структурной схемы заменяются своими эквивалентными
схемами замещения. Формирователи импульсов ФИ, а так же фиксаторы объединяются
с расположенными следом за ними непрерывными частями НЧ с образованием приведенных
непрерывных частей ПНЧ.
2.
Дискретизация выхода. Выходной сигнал
системы рассматривается только в дискретные моменты времени tk=kT0. Формально это соответствует размещению фиктивного ключа в
цепи наблюдения на выходе непрерывной части и не влияет на вид процессов в
системе.
3.
Структурные преобразования. Выполняются
допустимые преобразования полученной выше промежуточной структурной схемы.
4.
Определение дискретных звеньев.
Выявляются участки структурной схемы, для которых как входы, так и выходы
являются дискретными сигналами. Эти участки структурной схемы объявляются
дискретными звеньями.
Применим данный метод для исходной
структуры.
1) Замещение
Представим эквивалентные схемы
замещения для устройств дискретного действия.
а) АЦП

б) ЦВУ

в) ЦАП
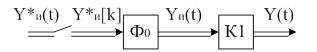
2) Дискретизация выхода
Разместим фиктивный ключ в цепи
наблюдения на выходе непрерывной части.

3) Структурные преобразования.
Выполним допустимые структурные
преобразования.
Ключ с выхода сумматора перенесем
на его входы.
Коэффициенты К1 и К2
удовлетворяют условию К2=1/К1.
Последовательность фиксатора и
непрерывной части представляют собой приведенную непрерывную часть.
Последовательно расположенные
фиксатор и ключ не изменяют дискретного сигнала.
4) Определение дискретных звеньев.
Последовательно соединенные ПНЧ и
ключ образуют дискретное звено приведенной непрерывной части ДЗПНЧ.
Таким образом, изобразим расчетную
структурную схему:
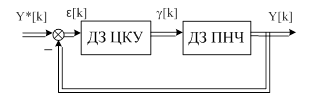
Рисунок 2.2 – Расчетная
структурная схема
2.2 Период дискретизации To. Дискретные
передаточные матрицы диагонального регулятора и компенсатора
Согласно методу аналогового
прототипа, шаг дискретизации То можно определить, зная частоту среза ср и запас устойчивости по фазе зап автономных каналов регулирования
непрерывной МСАР с обратными перекрестными связями в компенсаторе.
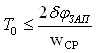 ;
;
Здесь δ –
допустимое уменьшение запаса устойчивости по фазе. Зададимся значением 6%.
Используя данные
пункта 1.4.3 определим шаг дискретизации для каждого из автономных каналов.
 ,
, 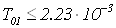 с,
с,
 ,
, 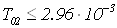 с.
с.
Выберем из полученных значений
шага дискретизации меньшее. Расчетное значение периода дискретности цифровой
МСАР
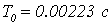 .
.
Согласно методу аналогового
прототипа и аппроксимации интеграторов по методу трапеций определим дискретные
передаточные матрицы «диагонального» регулятора и компенсатора.
Осуществим следующую замену:
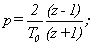
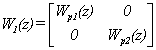 ,
,
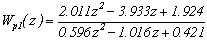 ,
,
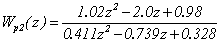
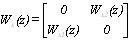 .
.
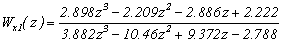 ,
,
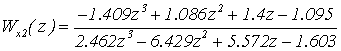
2.3
Переходные характеристики МСАР относительно пар «вх1-вых1» и «вх1-вых2»
Далее проведем сравнение
переходных характеристик автономной МСАР с обратными перекрестными связями в
компенсаторе и цифровой МСАР с обратными перекрестными связями в компенсаторе.
Переходные характеристики автономной МСАР с прямыми перекрестными связями в
компенсаторе после корректировки совпадают с переходными характеристиками
автономной МСАР с обратными перекрестными связями в компенсаторе, так как и в
том, и в другом случаях наблюдается абсолютная автономность.
Методом компьютерного моделирования
в программном пакете VisSim получим переходные характеристики относительно пар «вх1-вых1»
и «вх1-вых2» непрерывной МСАР с обратными ПС в компенсаторе. (Приложение 10)
Для получения переходных
характеристик цифровой МСАР проведем некоторое структурное преобразование.
Рассчитаем передаточную матрицу компенсатора и включим в систему
непосредственно его.
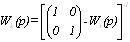 ,
,
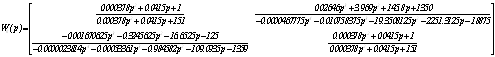
Сравним графики переходных
характеристик относительно пар «вх1-вых1» для непрерывной и дискретной МСАР
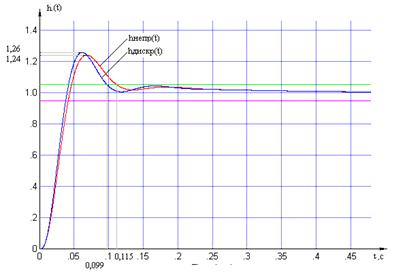
Рисунок 2.3 – Переходные
характеристики относительно пар «вх1-вых1» для дискретной и непрерывной МСАР
Определим время переходного
процесса и перерегулирование для каждого из вариантов:
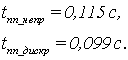

Можно отметить, что прямые
показатели качества переходного процесса непрерывной МСАР лучше, несмотря на
то, что время переходного процесса в данном случае у дискретной МСАР меньше,
так как его определение проводилось на уровне 5%. Если увеличить требования к
точности, то время переходного процесса для дискретной МСАР увеличится
значительнее, нежели для непрерывной МСАР.
Сравним графики переходных
характеристик относительно пар «вх1-вых2» для непрерывной и дискретной МСАР
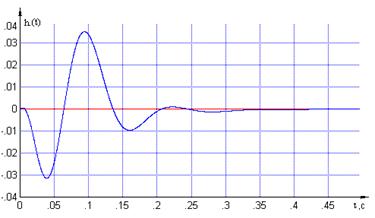
Рисунок 2.3 – Переходные
характеристики относительно пар «вх1-вых2» для дискретной и непрерывной МСАР
График переходной
функции дискретной МСАР относительно пары «вх.
1 – вых. 2» не совпадает с
аналогичным графиком переходной функции непрерывной МСАР. Это свидетельствует о
грубой автономности каналов регулирования цифровой МСАР.
Определим
подбором на модели новое расчетное значение шага дискретизации 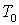 , при котором свойство
автономности для цифровой САР можно считать практически выполненным.
, при котором свойство
автономности для цифровой САР можно считать практически выполненным.
Увеличим шаг
дискретизации. Получим переходные характеристики для 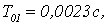
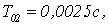
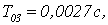
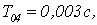
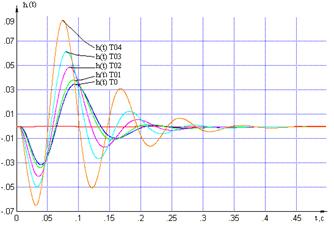
Рисунок 2.4 – Переходные
характеристики относительно пар «вх1-вых2» для дискретной МСАР с различными То
Попытка увеличить
шаг дискретизации приводит к увеличению максимального отклонения управляемой
величины от установившегося значения и времени установления.
Уменьшим шаг
дискретизации. Получим переходные характеристики для 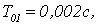
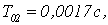
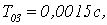
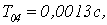
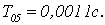 (Рисунок 2.5)
(Рисунок 2.5)
Из графиков
видно, что уменьшая шаг дискретизации можно добиться уменьшения максимального
отклонения управляемой величины от установившегося значения. Оптимальное
значение 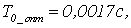 так как в этом случае наблюдается минимальное значение hmax(t), в то же время достаточно быстро достигается установившееся
значение.
так как в этом случае наблюдается минимальное значение hmax(t), в то же время достаточно быстро достигается установившееся
значение.
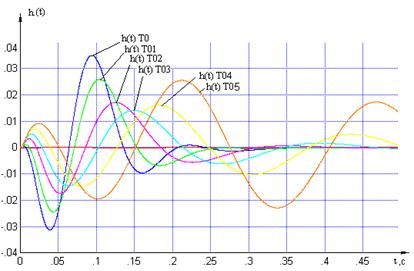
Рисунок 2.5 – Переходные
характеристики относительно пар «вх1-вых2» для дискретной МСАР с различными То
Таким образом, при 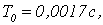 автономность является менее
грубой, при таком значении шага дискретизации свойство автономности можно
считать практически выполненным
автономность является менее
грубой, при таком значении шага дискретизации свойство автономности можно
считать практически выполненным
2.4
Устойчивость цифровой МСАР
Запишем
передаточную матрицу приведенной непрерывной части:
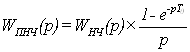 ,
,
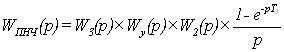 . (2.1)
. (2.1)
Запишем частотную передаточную
матрицу ДЗ ПНЧ:
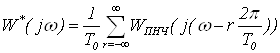 , (2.2)
, (2.2)
где 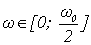 ,
здесь
,
здесь 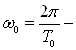 частота дискретизации.
частота дискретизации.
Определим значение частоты
дискретизации:
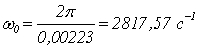
Получим передаточную матрицу
цифрового корректирующего устройства по методу трапеций подстановкой 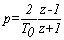 :
:
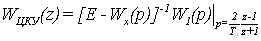 (2.3)
(2.3)
Частотно-передаточная матрица
разомкнутой системы запишется в виде
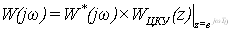
Определитель матрицы возвратных
разностей:
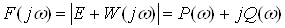
Построим обобщенный годограф Найквиста
с помощью MathCAD.
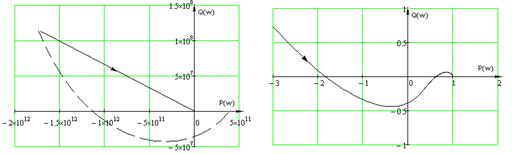
а) б)
Рисунок 2.6 – Обобщенный годограф
Найквиста цифровой МСАР
а) общий вид годографа Найквиста
б) построение годографа в области
высоких частот;
Разомкнутая система не имеет
правых корней характеристического уравнения, поэтому для устойчивости замкнутой
МСАР необходимо и достаточно, чтобы обобщенный годограф Найквиста, дополненный
на участке разрыва дугой бесконечно большого радиуса, не охватывал точку с
координатами (0; j0). Так как обобщенный годограф Найквиста, дополненный на
участке разрыва дугой бесконечно большого радиуса, не охватывает точку с
координатами (0; j0), то цифровая МСАР при 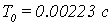 является
устойчивой.
является
устойчивой.
Проверим устойчивость цифровой
МСАР с помощью обобщенного критерия Найквиста при увеличенном в три раза расчетном
значении 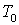 :
:
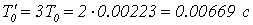
Передаточную
матрицу приведенной непрерывной части, частотную
передаточную матрицу ДЗ ПНЧ, дискретную передаточную матрицу цифрового корректирующего
устройства определим по формулам (2.1) – (2.3).
Построим годограф Найквиста с
помощью программного пакета MathCAD.
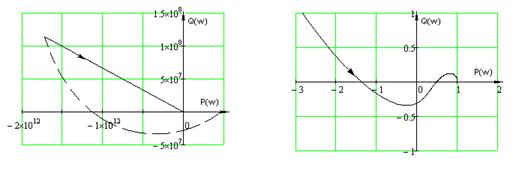
а) б)
Рисунок 2.7 – Обобщенный годограф
Найквиста цифровой МСАР
а) общий вид годографа Найквиста
б) построение годографа в области
высоких частот;
Разомкнутая система не имеет
правых корней характеристического уравнения, поэтому для устойчивости замкнутой
МСАР необходимо и достаточно, чтобы обобщенный годограф Найквиста, дополненный
на участке разрыва дугой бесконечно большого радиуса, не охватывал точку с
координатами (0; j0). Так как обобщенный годограф Найквиста, дополненный на
участке разрыва дугой бесконечно большого радиуса, не охватывает точку с
координатами (0; j0) (см. рисунок 2.17 б)), то цифровая МСАР при 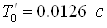 является устойчивой, но
запасы устойчивости системы уменьшаются (обобщенный годограф Найквиста при
является устойчивой, но
запасы устойчивости системы уменьшаются (обобщенный годограф Найквиста при 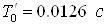 пересекает координатные
оси плоскости ближе к точке (0; j0), чем при
пересекает координатные
оси плоскости ближе к точке (0; j0), чем при 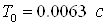 ).
).
2.5 Реакция цифровой МСАР на
гармоническое воздействие
Получим реакцию цифровой МСАР по
первому каналу на гармоническое воздействие с частотой w1=9.9 и сравним ее с аналогичной реакцией первого сепаратного
канала.
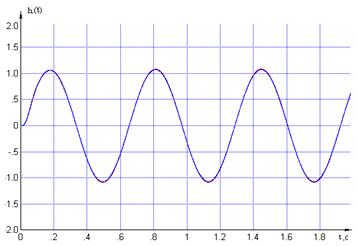
Рисунок – Реакция цифровой МСАР по
первому каналу и первого сепаратного канала на гармоническое воздействие с
частотой w1=9.9.
Сравним амплитуды колебаний выходного
сигнала первого канала цифровой МСАР и первого сепаратного канала:
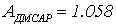
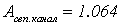
Таким образом, можно сделать вывод
о достаточно высокой точности МСАР, так как реакции цифровой МСАР по первому
каналу на гармоническое воздействие практически совпадает с реакцией на
аналогичное воздействие первого сепаратного канала, амплитуды колебаний
выходных сигналов различаются незначительно.
Библиографический список
1.
СТО ЮУрГУ 04–2008 Стандарт организации.
Курсовое и дипломное проектирование. Общие требования к содержанию и оформлению
/ составители: Т.И. Парубочная, Н.В. Сырейщикова, В.И. Гузеев, Л.В. Винокурова. –
Челябинск: Изд-во ЮУрГУ, 2008, – 56 с.
2.
Автоматизированное проектирование
систем автоматического управления /.А. Алексанкин, А.Е. Бржозовский, В.А. Жданов
и др.; под ред. В.В. Солодовнива. – М.: Машиностроение, 1990. – 335 с.
3.
Автоматизированное управление
технологическими процессами: учебное пособие / Н.С. Зотов, О.В. Назаров,
Б.В. Петелин, В.Б. Яковлев; под ред. В.Б. Яковлева. – Л.: Изд-во
ЛГУ, 1988. – 224 с.
4. Александров, А.Г. Синтез
регуляторов многомерных систем/ А.Г. Александров. – М.:
Машиностроение, 1986. – 272 с.
5. Баранчук, Е.И. Взаимосвязанные и
многоконтурные регулируемые системы Баранчук. – Л.: Энергия, 1968. – 267 с.
6. Барковский, В.В. Методы синтеза
систем управления/ В.В. Барковский, Н., Захаров, А.С. Шаталов. – М.:
Машиностроение, 1969. – 325 с.
7. Бусленко, Н.П. Лекции по теории
сложных систем / Н.П. Бусленко и др. – М.: Сов. радио, 1973.
8. Васильев, В.Н. Многоуровневое
управление динамическими объектами / Васильев и др. – М.: Наука, 1987.
9. Воронов, А.А. Введение в
динамику сложных систем управления / – М.: Наука, 1985.
10. Зырянов, Г.В. Системы управления многосвязными
объектами: учебное пособие / Г.В. Зырянов. – Челябинск: Издательский
центр ЮУрГУ, 2010.
11. Катковник, В.Я. Многомерные дискретные системы
управления / В.Я. Катковник, Р.А. Полуэктов. – М.: Наука, 1966.
– 416 с.
12. Морозовский, В.Т. Многосвязные системы
автоматического регулирования/ В.Т. Морозовский. – М.: Энергия, 1970. –
288 с.
13. Острем, К. Введение в стохастическую теорию
управления/ К. Острем. – М.: Мир, 1973. – 320 с.
14. Рэй, У. Методы управления технологическими
процессами / У. Рэй. – М.: 1983.
15. Соболев, О.С. Методы исследования линейных
многосвязных систем – М.: Энергоатомиздат, 1985. – 464 с.
16. Чинаев, П.И. Методы анализа и синтеза многомерных
автоматических систем / П.И. Чинаев. – Киев: Техника, 1969. – 377 с.
17. Янушевский, Р.Т. Теория линейных оптимальных
многосвязных систем управления / Р.Т. Янушевский. – М.: Наука, 1973. –
464 с.
18. Зырянов, Г.В. Линейные дискретные системы
управления / Г.В. Зырянов. – Минск: Изд-во ЮУрГУ, 2005. – 109 с.