Курсовая работа: Расчет и конструирование элементов рабочей площадки
Федеральное
агентство по образованию
Ангарская
государственная техническая академия
Кафедра
промышленного и гражданского строительства
Пояснительная
записка
по
курсовой работе
по
металлическим конструкциям
на тему: «Расчет
и конструирование элементов рабочей площадки»
Выполнил
Студент гр.
ПГС – 07 - 1
Очаковская Ю.
А.
Проверил
Савенков А.И.
Ангарск 2010
Исходные данные
Вариант – 3.1.2.
Схема поперечника рабочей
площадки приведена на рисунке 1.
Схема поперечника рабочей
площадки
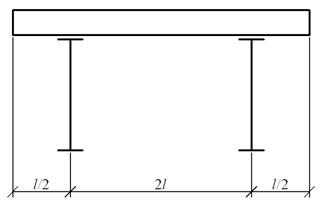
Рис. 1.
Размеры площадки в плане
– 2L x 3B
Шаг колонн в поперечном
направлении, L (м) – 12
Шаг колонн в продольном
направлении, В (м) – 6
Отметка чистого пола
первого этажа – ±0.000
Отметка верха настила – +8.400
Отметка верха габарита
помещения под рабочей площадкой – +6.200
Нормативная полезная
нагрузка (кН/м2) – 20
Характер действия
полезной нагрузки – статическая
Расчетная температура – -350
Сечение колонн – сквозная
Материал настила – ж/б
Класс бетона фундаментов
– В10
Способы соединения
элементов конструкций:
- заводские – сварка;
- монтажные – сварка,
болты.
Монтажный стык главной
балки запроектировать в середине или 1/3 пролета.
Марка стали – С255
Rу = 24,5 кН/см2
Ru = 37 кН/см2
1.
Технико-экономическое обоснование балочной клетки
Расстановка колонн и
главных балок устанавливается заданием. Поэтому основными факторами,
определяющими экономичность вариантов, является компоновочная схема и ее параметры.
1.1. Выбор
компоновочной схемы
Различают три вида
балочных клеток: упрощенный, нормальный и усложненный. Необходимо сравнить
нормальный (рис. 2.1.1) и усложненный (рис. 2.1.2) варианты балочных клеток.
При железобетонном
настиле шаг балок настила – назначается 1,5–3 м, шаг вспомогательных балок
назначается – 3-5 м.
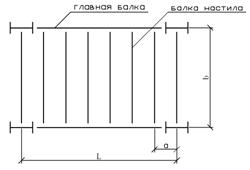
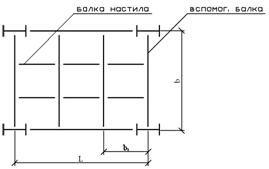
Рис.1.1.1. Простая балочная
клетка Рис.1.1.2. Усложненная балочная клетка
1. 2. Расчет настила
Материала настила –
железобетон. Толщина и максимальный расчетный пролет определяется в зависимости
от величины временной нормативной нагрузки по таблице 2.1.1. При этом для снижения
суммарной стоимости настила и поддерживающих балок, толщина плиты принимается
минимальной.
Таблица 1.2.1 Толщина и пролет железобетонной плиты
| Расчетный пролет плиты, м |
Толщина плиты (в см.) при временной нормативной нагрузке,
кПа (кН/м2)
|
| менее 15 |
20 и более |
менее 25 |
от 25 до 30 |
30 и более |
| <=1,5 |
8 |
8 |
12 |
12 |
14 |
| <=2,0 |
10 |
10 |
| <=2,5 |
12 |
14 |
16 |
| <=3,0 |
12 |
14 |
14 |
16 |
18 |
Толщина настила, t = 10 cм
Расчетный пролет плиты = 2,0 м
Нормативная величина
нагрузки от собственного веса настила 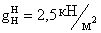
1.3. Расчет балок
настила и вспомогательных балок
В работе и расчете балок
настила и вспомогательных балок нет принципиальных различий, кроме вопросов
определения действующих нагрузок и обеспечения общей устойчивости.
1.3.1. Определение
нормативных и расчетных нагрузок
Нормативная и расчетная
величины равномерной и распределенной нагрузки, действующей на балки настила,
могут быть определены по формулам:
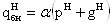
где α – шаг балок
настила, м;
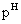 - нормативная величина полезной
нагрузки,
- нормативная величина полезной
нагрузки, 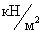
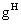 - нормативная величина нагрузки от
собственного веса настила,
- нормативная величина нагрузки от
собственного веса настила, 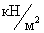
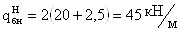
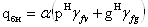
где 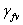 - коэффициент надежности
по нагрузке для временной нагрузки, принимаемый:
- коэффициент надежности
по нагрузке для временной нагрузки, принимаемый: 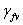 =
1,2
=
1,2
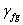 - коэффициент надежности для
постоянной нагрузки, принимаемый:
- коэффициент надежности для
постоянной нагрузки, принимаемый:
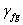 = 1,1
= 1,1
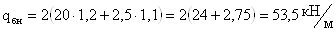
1.3.2 Определение
усилий и подбор сечения простой балочной клетки
В однопролетной разрезной
балке (расчетная схема рис. 1.3.2.1) действуют усилия:
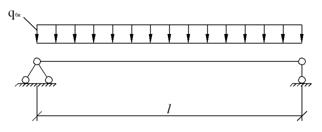
Рис. 1.3.2.1. Расчетная
схема балок.
Расчетный изгибающий
момент - 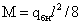
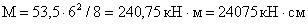
Нормативный изгибающий
момент - 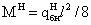
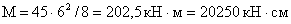
Поперечная сила - 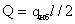
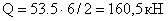
Балки настила могут
работать упруго или при органичном развитии пластических деформаций. Учет
пластической работы материала допускается в балках сплошного сечения, несущих
статическую нагрузку, у которых величина касательных напряжений в расчетом
сечении τ ≤ 0,9 Rу. При этом предполагается, что
пластические деформации локализуются в узкой зоне около наиболее нагруженного
сечения в середине однопролетной балки, загруженной равномерно распределенной
нагрузкой.
Балки настила, несущие
динамическую нагрузку, и вспомогательные балки работают упруго. Их предельное
состояние наступает при достижении максимальными по величине нормальными или
касательными напряжениями значений Rу или RS соответственно. При этом нормальные
напряжения определяют в крайних волокнах сечения с максимальным изгибающим
моментом, а касательные – по нейтральной оси опорного сечения.
Номер прокатного профиля
балки можно определить по прочности (из условия равенства величины максимальных
нормальных напряжений расчетному сопротивлению стали растяжению, сжатию) или по
жесткости (из условия равенства фактического прогиба величине предельно допустимого
прогиба).
Поскольку основной
единицей измерения, является сантиметр, для удобства вычислений при выполнении
конструктивных расчетов следует перейти от размерности, кН м, в которой ранее
были определены усилия, к размерности кН см, для чего величины моментов нужно
умножить на 100, Rу, в МПа разделить на 10, модуль
продольных деформаций принять равным Е = 20600 кН/см2.
Требуемый момент
сопротивления поперечного сечения балки, определенной по прочности, равен: при
упругой работе:
Wreq = M/(Rу ∙ γc),
где Rу – расчетное сопротивление стали при
растяжении, сжатии, изгибе, определенное по пределу текучести.
γc – коэффициент условия работы,
принимаемый равный 1.
Wreq = 24075/1,12*24,5= 877,37 см3
По полученной упругой
работе подбираем профиль проката:
Профиль – 40Б2
Н = 39,6 см
bf = 16.5 см
tw = 0.75 cм
tf = 1,15 см
А = 69,72 см2
Iх = 18530 см4
Wх = 935,7 см3
Линейная плотность =
0,548 кН/м
Sх = 529,7 см3
It = 33,094 см4
1.3.3 Проверка
принятого профиля простой балочной клетки
Проверка принятого
сечения балки следует выполнять:
- по уточненным нагрузкам,
определенным с учетом дополнительной нагрузки от собственного веса балки;
- по расчетному
сопротивлению стали, уточненному в зависимости от фактической толщины проката,
равной толщине полки балки;
- по фактическим
статическим характеристикам сечения балки.
Усилия, уточненные с
учетом действия дополнительной нагрузки от собственного веса балки (в
размерности кН м, кН):
- изгибающий момент
нормативный
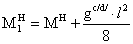
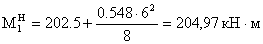
- изгибающий момент
расчетный
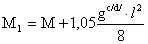
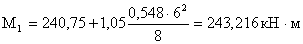
- поперечная сила
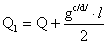
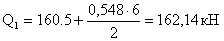
Проверка нормальных
напряжений
- При расчете в
упругой стадии
Максимальная величина
нормальных напряжений, действующих в середине пролета:
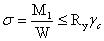
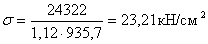 =>
=> 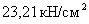 <
< 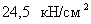 -
-
условие выполнилось
Проверка
касательных напряжений
Касательные напряжения
следует определять и проверять в опорном сечении:
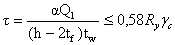
где 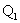 - опорная реакция балки.
- опорная реакция балки.
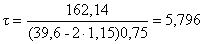 => 5,796 < 14,21 – условие выполнилось.
=> 5,796 < 14,21 – условие выполнилось.
Проверка жесткости
Проверка жесткости балки
производится по формуле:
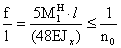
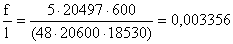 => 0,00336 < 0,005 –
=> 0,00336 < 0,005 –
условие выполнилось.
1.3.4 Определение
усилий и подбор сечения усложненной балочной клетки (балки настила)
В однопролетной разрезной
балке (расчетная схема рис. 2.3.4.1) действуют усилия:
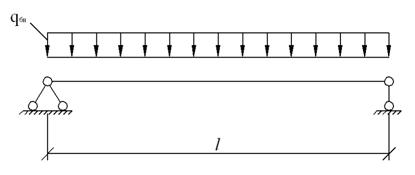
Рис. 1.3.4.1. Расчетная
схема балок.
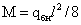
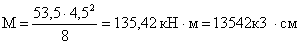
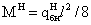
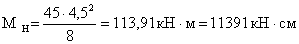
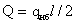
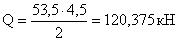
Wreq = M/(Rу ∙ γc)
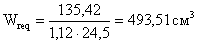
По полученной упругой
работе подбираем профиль проката:
Профиль – 35Б1
Н = 34,6 см
bf = 15,5 см
tw = 0,62 cм
tf = 0,85 см
А = 49,53 см2
Iх = 10600 см4
Wх = 581,7 см3
Линейная плотность = 0,389
кН/м
Sх = 328,6 см3
It = 14,843 см4
1.3.5 Проверка
принятого профиля усложненной балочной клетки (балки настила)
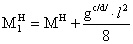
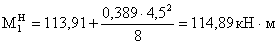
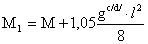
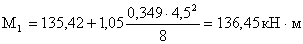
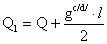
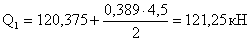
Проверка нормальных
напряжений
- При расчете в
упругой стадии
Максимальная величина
нормальных напряжений, действующих в середине пролета:
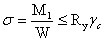
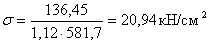 =>
=> 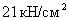 <
< 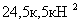 - условие выполнилось
- условие выполнилось
Проверка
касательных напряжений
Касательные напряжения
следует определять и проверять в опорном сечении:
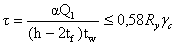
где 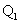 - опорная реакция балки.
- опорная реакция балки.
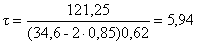 => 6 < 14,21 – условие выполнилось.
=> 6 < 14,21 – условие выполнилось.
Проверка жесткости
Проверка жесткости балки
производится по формуле:
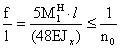
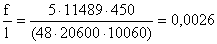 => 0,0026 < 0,005 – условие выполнилось.
=> 0,0026 < 0,005 – условие выполнилось.
1.3.6 Определение
усилий и подбор сечения усложненной балочной клетки (вспомогательной балки)
В однопролетной разрезной
балке (расчетная схема рис. 2.3.4.1) действуют усилия:
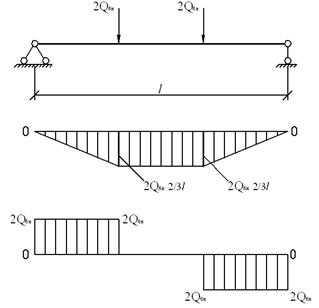
Рис. 1.3.6.1. Расчетная
схема балок.
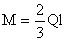
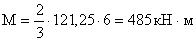
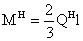
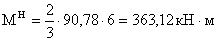
Q1 = 121,25 кН
Wreq = M/(Rу ∙ γc)
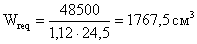
По полученной упругой
работе подбираем профиль проката:
Профиль – 55Б1
Н = 54,3 см
bf = 20 см
tw = 0,95 cм
tf = 1,35 см
А = 113,37 см2
Iх = 55680 см4
Wх = 2051 см3
Линейная плотность =
0,891 кН/м
Sх = 1165 см3
It = 73,366 см4
1.3.5 Проверка
принятого профиля усложненной балочной клетки (вспомогательной балки)
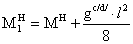
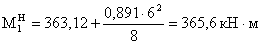
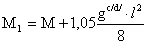
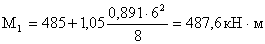
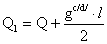
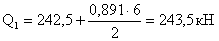
Проверка нормальных
напряжений
- При ограниченном
развитии пластических деформаций
Максимальная величина
нормальных напряжений, действующих в середине пролета:
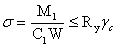
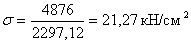 =>
=> 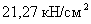 <
< 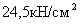 -
-
условие выполнилось
Проверка
касательных напряжений
Касательные напряжения
следует определять и проверять в опорном сечении:
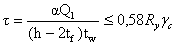
где 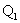 - опорная реакция балки.
- опорная реакция балки.
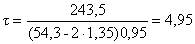 => 5 < 14,21 – условие выполнилось.
=> 5 < 14,21 – условие выполнилось.
Проверка жесткости
Проверка жесткости балки
производится по формуле:
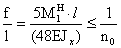
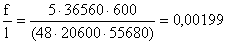 => 0,002 < 0,005 – условие выполнилось.
=> 0,002 < 0,005 – условие выполнилось.
1.4 Выбор оптимального
варианта
Для принятия варианта
компоновки балочной клетки производится сравнение вариантов по расходу
материалов, стоимости и количеству элементов, результаты которого заносятся в
таблицу 2.4.1. В качестве определяющего показателя при выборе оптимального
варианта принимается расход стали (кг/см2) или стоимость материала
конструкций (руб./м2). В том случае, если расход стали или стоимость
по вариантам отличаются менее чем на 5%, в качестве оптимального варианта
принимается вариант с меньшим количеством монтажных элементов. Выявленный на
основании сравнения оптимальный вариант принимается к дальнейшей разработке.
Таблица 1.4.1
Сравнение вариантов
балочной клетки
| Наименование |
Простая балочная клетка |
Усложненная балочная клетка |
|
Расход стали, кг/м2
|
Количество балок |
Масса стали, кг |
Расход стали, кг/м2
|
Количество балок |
Масса стали, кг |
| Одной балки |
Всех балок |
Одной балки |
Всех балок |
| Балки настила |
28,41 |
84 |
54,8 |
4603,2 |
12,97 |
72 |
38,9 |
2800,8 |
| Вспом. Балки |
|
|
|
|
21,45 |
39 |
89,1 |
3474,9 |
| Итого |
28,41 |
|
34,42 |
|
2. Расчет главной
балки
Главная балка проектируется
составного сварного семеричного двутаврового сечения.
2.1 Определение
нормативных и расчетных нагрузок
При действии на балку
более 4-х сосредоточенных сил, нагрузка принимается равномерно -
распределенной. Выделим две составляющие этой нагрузки:
- составляющая, вызванная
действием временной нагрузки
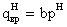
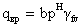
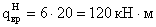
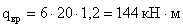
- составляющая, вызванная
действием постоянной нагрузки (собственный вес конструкций)
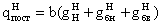
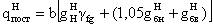
где b – шаг главных балок (м),
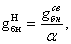
нормативная нагрузка от
собственного веса балок настила и вспомогательных балок (кН/м2).
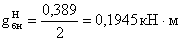
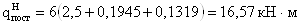
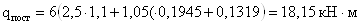
2.2. Определение
усилий
В двухконсольной балке
при действии равномерно-распределенной нагрузки максимальный пролетный и
изгибающий момент:
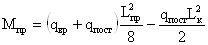
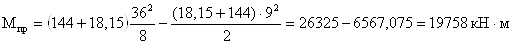
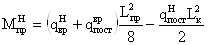
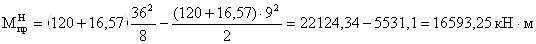
- максимальный опорный
момент
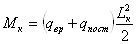
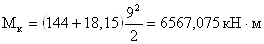
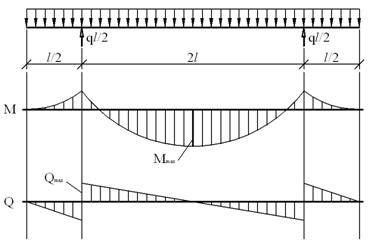
Рис.22.1. Эпюры моментов
и поперечных сил в двухконсольной балке
Поперечная сила,
действующая в опорном сечении со стороны консоли:
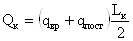
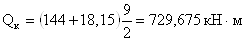
- в опорном сечении со
стороны пролета:
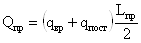
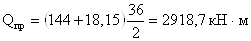
Максимальная величина
опорной реакции двухконсольной балки:
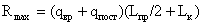
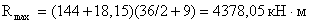 .
.
2.3 Компоновка сечения
Компоновка сечения, то
есть определение размеров элементов в пределах принятого типа сечения
(Рис.3.3.1.), является технико-экономической задачей: необходимо выбрать
размеры элементов сечения из предлагаемого перечня (сортамента) таким образом,
чтобы удовлетворялись условия прочности, жесткости, общей и местной
устойчивости, конструктивные требования и, в то же время, принятое сечение
имело минимальный вес.
Из определяемых параметров
сечения (hw, t w, bf и tf) наибольшее влияние на вес оказывает
высота стенки балки hw или близкая к ней высота сечения h.
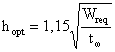 ,
,
где 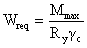 ,
,
толщина стенки
принимается: t w = 2см.
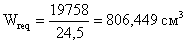
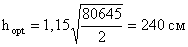
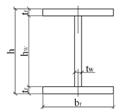
Рис. 2.3.1. Составное
сечение главной балки
Кроме оптимальной высоты,
существует минимальная высота, определяемая из условия обеспечения требуемой
жесткости балки:
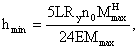
где n0 – величина обратная предельному относительному
прогибу, для главных балок рабочих площадок, несущих технологические нагрузки,
n0 = 300
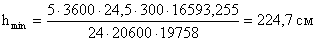
Требуемая площадь сечения
пояса:
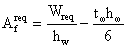
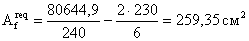
Ширина пояса, которая
обеспечивает общую устойчивость балки и равномерное распределение нормальных
напряжений по ширине пояса:
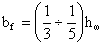
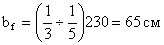
Толщина пояса: 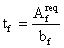 , при этом должны
соблюдаться условия:
, при этом должны
соблюдаться условия:
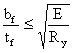 и tf ≤ 3tw
и tf ≤ 3tw
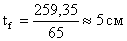
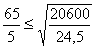
13 < 29 – условие выполнилось.
5 < 6 - условие выполнилось.
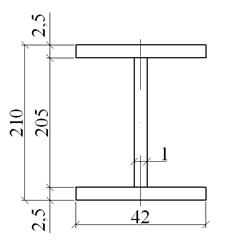
Рис. 2.3.2. Составное
сечение главной балки
2.4. Проверка
нормальных напряжений
Геометрические
характеристики принятого сечения: -
площадь:
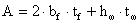
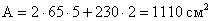
- момент инерции:
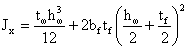
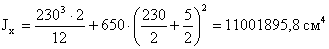
- момент сопротивления:
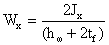
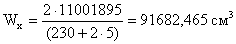
Проверку нормальных
напряжений следует выполнять:
- по расчетным
сопротивлениям стали, уточненным в зависимости от фактической толщины полки
балки;
- по усилиям,
определенным с учетом собственного веса балки.
Линейная нагрузка от собственного
веса главной балки:
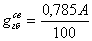
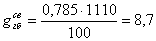 кН/м
кН/м
Дополнительные изгибающие
моменты в пролете двухконсольной балки:
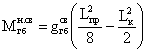
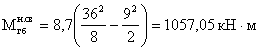
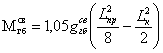
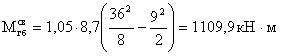
Дополнительный опорный
момент:
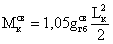
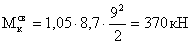
Дополнительная поперечная
сила, действующая в опорном сечении со стороны консоли:
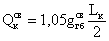
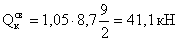
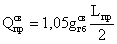
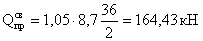
Опорная реакция
двухконсольной балки от собственного веса
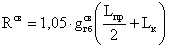
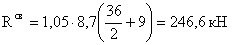
Усилия, уточненные с
учетом действия дополнительной нагрузки от собственного веса балки (в
размерности кНм, кН):
- изгибающие моменты
пролетные:
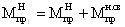
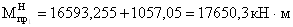
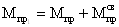
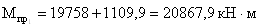
- момент опорный:
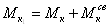
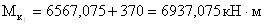
- поперечные силы:
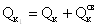
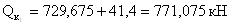
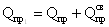
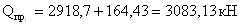
- опорная реакция:
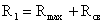
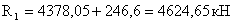
Нормальные напряжения
необходимо проверить в крайних волокнах сечения, где действуют максимальный
изгибающий момент:
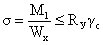
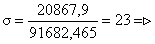 23 < 24,5 – условие выполнилось.
23 < 24,5 – условие выполнилось.
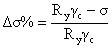
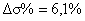 - условие выполнилось.
- условие выполнилось.
2.5. Проверка
жесткости
Относительный прогиб в
середине пролета двухконсольной балки:

где 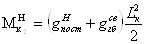
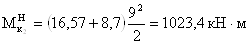
к = 1,05 – коэффициент,
учитывающий изменение жесткости балки по длине.
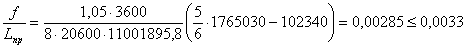 -
-
условие выполнилось.
2.6. Изменение сечения
балки по длине
Сечение балки изменяют в
целях экономии металла. В сварных балках конструктивно наиболее просто
изменение ширины пояса.
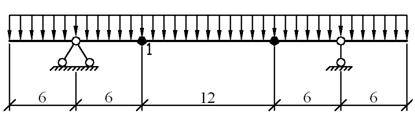
Рис.2.6.1. Место
изменения сечения главной балки
М1 = 6937,075кН
∙ м
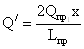
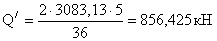
- требуемый момент
сопротивления измененного сечения:
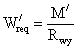
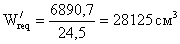
- требуемая площадь пояса
в измененном сечении:
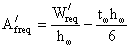
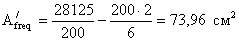
- ширина пояса в
измененном сечении:
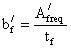
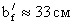
Для измененного
сечения балки вычисляют:
- площадь:
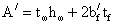
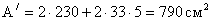
- момент инерции:
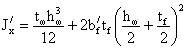
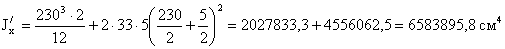
- момент сопротивления:
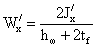
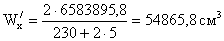
- статический момент
пояса относительно нейтральной оси:
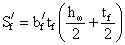
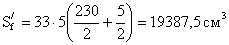
- статический момент
половины сечения относительно нейтральной оси:
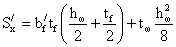
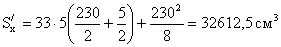
2.7. Проверка
прочности балки в измененном сечении
В вместе изменения
сечения балки необходимо проверить:
- наибольшие нормальные
напряжения:
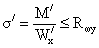
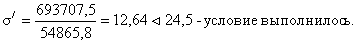
Приведенные напряжения на
уровне стыка пояса и стенки от совместного действия нормальных, касательных и
местных напряжений (Рис.3.7.1.).
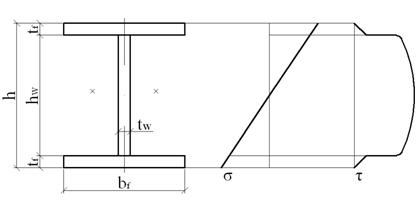
Рис.2.7.1. Эпюры
нормальных и касательных напряжений
Местные напряжения
отсутствуют, следовательно приведенные напряжения определяются по формуле:
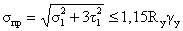
где 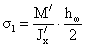 ;
; 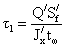
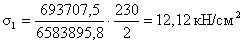
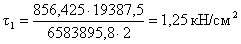
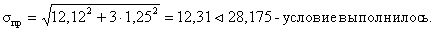
2.8. Проверка
касательных напряжений в опорном сечении
Максимальные касательные
напряжения в опорном сечении
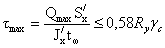
где Qmax – максимальная величина поперечной
силы в опорном сечении.
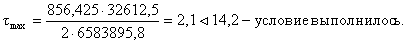
2.9. Проверка общей
устойчивости
Общая устойчивость балки
считается обеспеченной при передаче нагрузки через сплошной жесткий настил,
непрерывно опирающийся на верхний пояс балки и надежно с ним связанный, а так
же, если соблюдается условие:
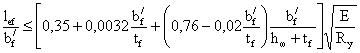
где 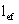 - расчетная длина, равная
расстоянию между точками закрепления верхнего пояса балки (шаг балок настила
или вспомогательных балок).
- расчетная длина, равная
расстоянию между точками закрепления верхнего пояса балки (шаг балок настила
или вспомогательных балок).
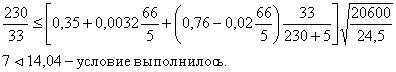
2.10. Проверка местной
устойчивости элементов балки
Местная устойчивость
сжатого пояса балки считается обеспеченной, если соблюдается условие:
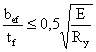
Устойчивость стенки балки
не требуется проверять, если условная гибкость стенки
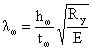
не превышает: 3,5 – при
отсутствии местных напряжений; 2,5 – при наличии местных напряжений в балках с
двусторонними поясными швами. При этом, если условная гибкость стенки превышает
величины: 3,2 – при отсутствии местной нагрузки и 2,2 – при наличии местной
нагрузки, то стенку балки необходимо укреплять поперечными ребрами жесткости.
Расстояние между ребрами жесткости не должно превышать 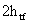 при
при 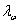 >3,2 и
>3,2 и 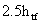 при
при 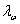 >3,2.
>3,2.
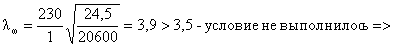
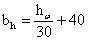
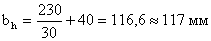
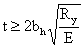
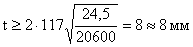

4,5 < 25 – условие
выполнилось.
При отсутствии местного
напряжения (под вспомогательными балками или балками настила стоят ребра
жесткости) – по формуле:
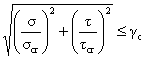
σ и τ
вычисляются по средним значениям изгибающего момента и поперечной силы для
наиболее напряженного участка с длиной, равной расчетной высоте отсека.
где  - нормальные напряжения,
- нормальные напряжения,
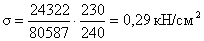
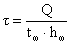 - касательные напряжения,
- касательные напряжения,
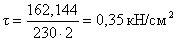
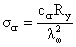 - критические нормальные напряжения,
- критические нормальные напряжения,
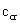 - коэффициент, принимаемый в
зависимости от коэффициента δ.
- коэффициент, принимаемый в
зависимости от коэффициента δ.
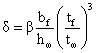 ,
,
где β – коэффициент,
принимаемый равным бесконечности – при непрерывном опирании жестких плит на
верхний сжатый пояс, в прочих β = 0,8.
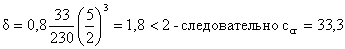
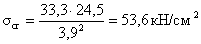
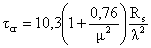 - критические касательные напряжения.
- критические касательные напряжения.
где 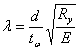 ; μ – отношение
большей стороны отсека к меньшей.
; μ – отношение
большей стороны отсека к меньшей.
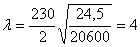
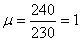
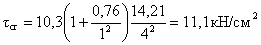
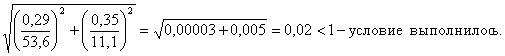
2.11. Определение
катетов поясных швов
Сварные поясные швы в
балках делаются сплошными одной толщины при помощи сварочных автоматов. По
конструктивным соображениям минимальный катет поясного шва принимается в
зависимости от толщины полки. Поясной шов принятого катета проверяется на
прочность по металлу шва
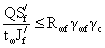
где 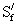 - статический момент пояса
балки относительной нейтральной оси, см3;
- статический момент пояса
балки относительной нейтральной оси, см3;
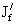 - момент инерции пояса балки
относительно нейтральной оси в измененном сечении, см4.
- момент инерции пояса балки
относительно нейтральной оси в измененном сечении, см4.
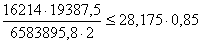
23,87 < 32,3
2.12. Конструирование
и расчет опорной части
Требуемая площадь
опорного ребра:
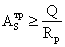
где Q – опорная реакция главной балки;
Rp=Ru – расчетное сопротивление стали
смятию торцевой поверхности.
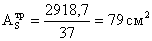
Принимаем толщину
опорного ребра ts = 20 мм
Определяем ширину ребра:
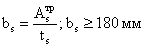
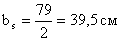 ,
,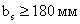 значит
значит 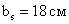
Проверяем устойчивость
опорного ребра:
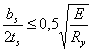
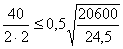
10 < 14,5 – условие
выполнилось.
Окончательную толщину
опорного ребра принимаем кратно 20 мм.
Опорную часть балки
проверяют на устойчивость из плоскости относительно оси Z:
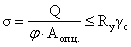
где 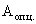 - расчетная площадь опорной
части балки;
- расчетная площадь опорной
части балки;
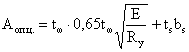
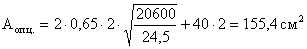
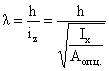
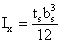
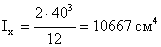
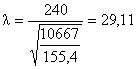
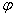 - коэффициент продольного изгиба,
- коэффициент продольного изгиба, 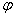 =0,894
=0,894
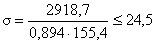
21 < 24,5 – условие
выполнилось.
Определяем толщину швов
прикрепления опорных ребер к стенке.
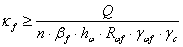
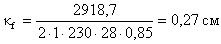
Минимальный
конструктивный шов – 6 мм.
2.13. Конструирование
и расчет монтажного стыка главной балки
Главная балка разбита на
3 отправочных элемента. Монтажный стык выполняется сварным или на высокопрочных
болтах.
При выполнении сварного
стыка в 1/3 пролета и соблюдении условия 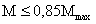 стыки
обоих поясов выполняются прямыми.
стыки
обоих поясов выполняются прямыми.
При выполнении сварных
швов рекомендуется применение электродов с индексом А, обеспечивающих
повышенную пластичность наплавленного металла.
При выполнении стыка на
высокопрочных болтах рекомендуется принимать один диаметр болтов для поясов стенки.
Основным является диаметр 20 мм. Стык выполняется при помощи накладок. Изгибающий момент в стыке распределяется между поясами и стенкой пропорционально их
жесткости. Доля изгибающего момента,
приходящегося на пояс:
Мf = Mст - Мω
Мст –
изгибающий момент в месте выполнения стыка,
Iω – момент инерции стенки,
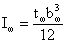
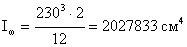
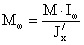
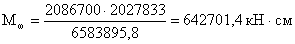
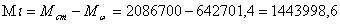
- усилие в поясных
накладках:
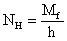
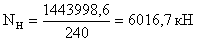
Требуемая площадь
накладки нетто:
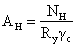
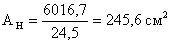
Необходимое количество
болтов с одной стороны стыка:
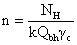
где k – количество поверхностей трения
соединяемых элементов, k = 1
– при одной накладке на поясе; k = 2
– при двух накладках на поясе; 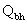 -
расчетное усилие, которое может быть воспринято каждой поверхностью трения
соединяемых элементов, стянутых одним высокопрочным болтом.
-
расчетное усилие, которое может быть воспринято каждой поверхностью трения
соединяемых элементов, стянутых одним высокопрочным болтом.
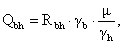
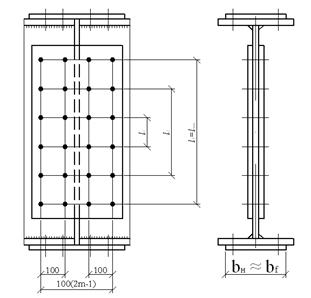
Рис. 2.13.2. Расположение
болтов на стенке балки
где 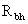 - расчетное сопротивление
растяжению высокопрочного болта;
- расчетное сопротивление
растяжению высокопрочного болта;
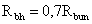
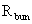 - наименьшее временное
сопротивление;
- наименьшее временное
сопротивление;
μ – коэффициент
трения;
γb – коэффициент условия работы соединения,
зависящий от количества болтов (n),
необходимых для восприятия расчетных усилий, принимается равным 0,8 при n < 5; 0,9 при 5 ≤ n < 10; 1,0 при n ≥
10;
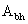 - площадь сечения болта нетто;
- площадь сечения болта нетто;
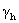 - коэффициент надежности.
- коэффициент надежности.
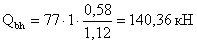
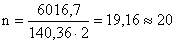
Толщина стыковой
площадки:
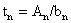
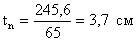
Проверяем прочность
поясных накладок, ослабленных отверстием под болты:
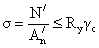
где 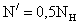 ;
;
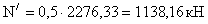
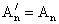
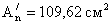
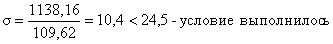 .
.
Определяем расстояние
между крайними горизонтальными рядами болтов:
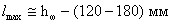
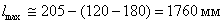
Количество вертикальных
рядов болтов:
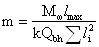
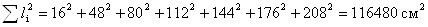
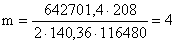
принимаем m = 4 вертикальных ряда с одной
стороны стыка.
При совместном действии
изгибающего момента и поперечной силы наибольшее усилие определяется как:
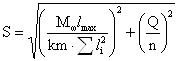
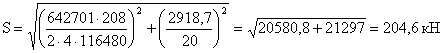
Для обеспечения прочности
соединения необходимо, чтобы:
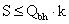
204,6 < 280,72 –
условие выполнилось.
3. Расчет колонны
Рассчитывается центрально
сжатая колонна среднего ряда. Сечение колонны может быть сплошным или сквозным
в соответствии с заданием. Сечение сквозной колонны компонуется из прокатных
двутавров, соединенных безраскосной решеткой на планках.
3.1. Расчет стержня
колонны сплошного сечения
Подсчитываем расчетную
сжимающую силу:
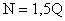
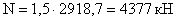
Геометрическая длина
колонны:
L = 8,400 + 0,6 - 2 = 7 м
Зададимся гибкостью
колонны: λ = 60, φ = 0,805
Требуемая площадь сечения
ветви:
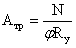
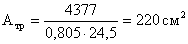
Принимаем ветви из двух
двутавров 55Б1: А = 226 см2; Ix = 37160 см4; Iу = 1630 см4 ix = 16 см; iу = 4,22 см; масса 1 м.п. = 0,890 кН
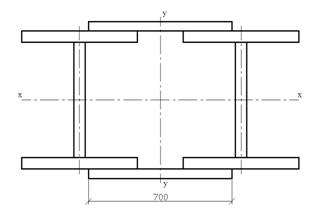
Рис. 3.1.1. Сечение
сквозной колонны
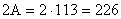 см2
см2
Гибкость колонны:

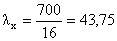 получаем
получаем 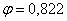
Проверка устойчивости
колонны относительно материальной оси:
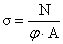
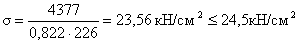 - условие выполнилось.
- условие выполнилось.
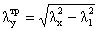
где 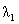 - гибкость ветви на участке
между планками относительно оси параллельной свободной, предварительно
принимаем 40.
- гибкость ветви на участке
между планками относительно оси параллельной свободной, предварительно
принимаем 40.
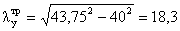
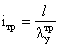
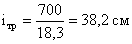
Расстояние между осями
ветви:
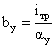
где 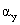 =0,52
=0,52
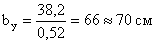
Толщину планки принимаем
равной 10 мм.
Размеры соединительных
планок:
- ширина планки:
bпл = 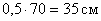
- длина планки:
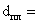 64 см
64 см
Момент инерции составного
сечения относительно свободной оси:
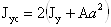
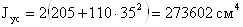
Радиус инерции составного
сечения:
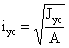
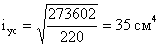
Гибкости:
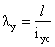
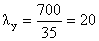
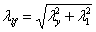
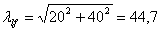 значит
значит 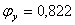
Проверка устойчивости
колонны относительно свободной оси:
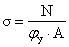
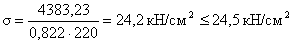
Устойчивость колонны
обеспечена.
3.2. Расчет планок
Условная поперечная сила:
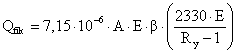
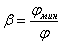
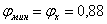 ;
; 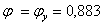
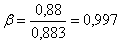
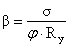
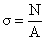
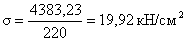
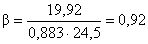
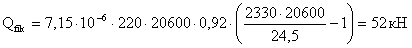
Изгибающий момент в
прикреплении планки:
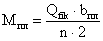
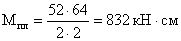
Поперечная сила в
прикреплении планки:
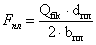
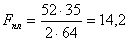 кН
кН
Равнодействующее
напряжение:
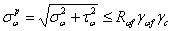
Нормальные напряжения от
изгиба шва:
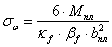
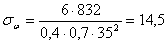 кН/см2
кН/см2
Касательные напряжения от
среза шва:
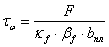
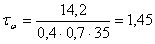 кН/см2
кН/см2
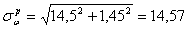 кН/см2 <
кН/см2 < 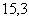 кН/см2 –
прочность сварных швов обеспечена.
кН/см2 –
прочность сварных швов обеспечена.
3.3. Расчет оголовка
колонны
Ширина опорного ребра
оголовка:
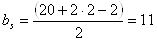 см
см
Требуемая площадь опорных
ребер:
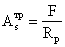 ,
,
где 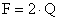
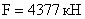
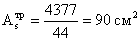
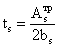
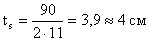
Длина опорного ребра
оголовка:
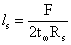
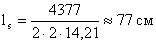
Определим высоту катета швов
прикрепления ребер к траверсе и траверсы к стенке:
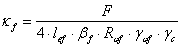
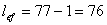 см
см
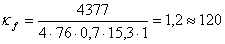 мм
мм
Высота траверсы:
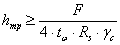
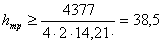 см
см
Толщина траверсы:
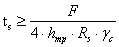
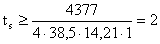 см
см
Cнизу траверсу укрепляем ребром
жесткости, ширину которого принимают равной 2bs+tmp=2*11+2=24 см, а толщину не менее
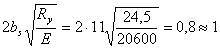 см
см
3.4. Расчет базы
колонны
Базу колонны проектируем
с траверсами для жесткого закрепления колонны в плоскости поперечной рамы и
шарнирного - в другой плоскости.
Требуемая площадь опорной
плиты базы определяется по формуле:
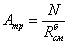
где 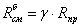 ;
; 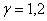 ;
; 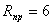 МПа
МПа
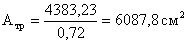
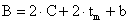
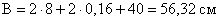
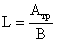
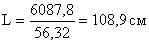 , принимаем L = 110 см, В = 70 см.
, принимаем L = 110 см, В = 70 см.
А = В ∙ L
А = 110 ∙ 70 = 7700
см2
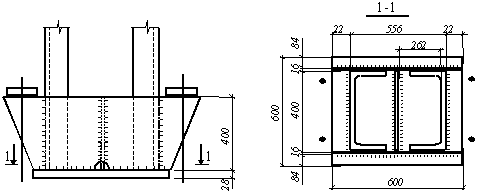
Рис. 3.4.1. База колонны
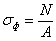
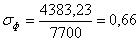 кН/см2
кН/см2
Изгибающий момент на
консольном участке:
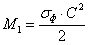
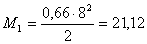 кН∙см
кН∙см
Изгибающий момент на
участке, опертом по трем сторонам: (а/b < 0,5):
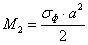
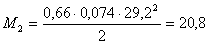 кН∙см
кН∙см
Изгибающий момент на участке,
опертом по четырем сторонам: (a/b < 0.5)
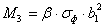
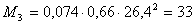 кН∙см
кН∙см
Толщина опорной плиты:
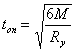
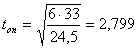 см, принимаем 28 мм.
см, принимаем 28 мм.
Высота траверсы:
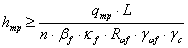
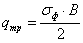
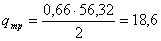 кН/см
кН/см
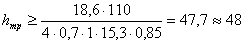 см
см
Проверяем нормальные
напряжения в пролете:
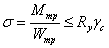
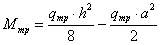
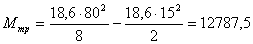 кН∙см
кН∙см
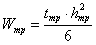
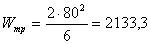 см3
см3
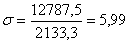 кН/см2 < 24,5 кН/см2
кН/см2 < 24,5 кН/см2
Толщина швов,
прикрепляющих траверсы и ребра к опорной плите kf = 0,6 см