Шпаргалка: Сопротивление материалов
Сопротивление
материалов.
1.
Какие
вопросы рассматриваются в дисциплине «Сопротивление материалов»?
В сопротивлении
материалов рассматриваются вопросы расчета отдельных элементов конструкций и
вопросы расчета некоторых простейших конструкций на прочность, жесткость и
устойчивость.
Прочность – способность
конструкции, а также ее частей и деталей выдерживать действие внешних нагрузок,
не разрушаясь.
Жесткость – способность
конструкции и ее элементов сопротивляться изменению своих первоначальных
размеров и формы.
Устойчивость –
способность конструкции и ее элементов сохранять определенную начальную форму
равновесия.
2.
Назвать
наиболее известных ученых в области науки «Сопротивление материалов»?
Роберт Гук (1635-1705) –
английский естествоиспытатель – открыл фундаментальную зависимость между силами
и вызываемыми перемещениями.
Симон Дени Пуассон
(1781-1840) – французский механик, физик и математик – впервые ввел коэффициент
Пуассона, который характеризует свойства материала.
Якоб Бернулли (1684-1705)
– швейцарский механик, физик – сформулировал гипотезу плоских сечений:
поперечные сечения стержня, плоские до деформации, остаются плоскими и после
деформации.
Журавский Д.И.
(1824-1891) – выдающийся инженер путей сообщения, строитель мостов – вывел
дифференциальную зависимость между изгибающим моментом и поперечной силой,
получил формулу для касательных напряжений в поперечных сечениях бруса.
Генрих Рудольф Герц
(1857-1894) – немецкий физик – впервые методами теории упругости решил задачу о
контактных (местных) напряжениях.
Леонард Эйлер (1707-1783)
– математик и механик – вывел формулу Эйлера для критической силы при расчете на
устойчивость продольно сжатого стержня.
Феликс Станиславович
Ясинский (1856-1899) – русский инженер и механик – вывел эмпирическую формулу
для критических напряжений при гибкости стержня меньше предельной (уточнил
область применимости формулы Эйлера).
3.
Основные
расчетные элементы в сопротивлении материалов.
Основными расчетными
типовыми элементами, на которые делится целая конструкция, являются стержень,
брус, оболочка, пластина, массивное тело, балка, ферма.
Стержень – тело, длина
которого существенно превышает характерные размеры поперечного сечения.
Брус – это тот же
стержень.
Балка – стержень или
брус, работающий на изгиб.
Пластина – тело, у
которого толщина существенно меньше двух других размеров.
Оболочка – тело,
ограниченное криволинейными поверхностями (искривленная пластина).
Массивное тело – элемент
конструкции с размерами одного и того же порядка.
Ферма – стержневая
конструкция, работающая только на растяжение или сжатие.
4.
Что
понимается под внутренними силовыми факторами и как они определяются ?
Под действием внешних
нагрузок в сечении конструкции (стержня, балки и т.д.) возникают дополнительные
усилия, которые называются внутренними силовыми факторами и которые
определяются методом сечения. Это реакция связи одной отсеченной части на
другую, реакция опоры на тело, реакция гибкой связи и др. Силы воздействия
отсеченной части на рассматриваемый элемент конструкции по отношению к нему
являются внешними силами и определяются по общим уравнениям равновесия.
5.
Какие виды
деформации бруса определяют внутренние силовые факторы ?
С помощью метода сечений
определяются внутренние силовые факторы: главный вектор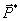 и главный момент
и главный момент 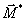 раскладываются на
составляющие
раскладываются на
составляющие 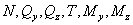 , которые определяют следующие
виды деформации:
, которые определяют следующие
виды деформации:
1) Растяжение (сжатие) –
продольная сила 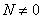 , а все остальные составляющие
равны нулю.
, а все остальные составляющие
равны нулю.
2) Сдвиг (срез) –
поперечная сила 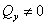 или
или 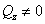 , а все остальные равны нулю.
, а все остальные равны нулю.
3) Кручение – крутящий
момент 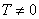 , а
все остальные равны нулю.
, а
все остальные равны нулю.
4) Изгиб – когда или 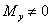 , или
, или 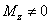 , а остальные
составляющие равны нулю.
, а остальные
составляющие равны нулю.
5) Сложное сопротивление
– когда сочетание каких-либо внутренних усилий не равно нулю.
6.
Что
понимается под механическим напряжением и какова его размерность ?
Напряжением на данной
площадке называется интенсивность внутренних сил, передающихся в точке через
выделенную площадку.
Полное напряжение 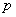 на данной
площадке раскладывается на нормальное
на данной
площадке раскладывается на нормальное 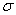 и касательное
и касательное 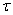 напряжения, причем
напряжения, причем 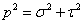 . Напряжение
имеет размерность интенсивности нагрузки, т.е. МПа (кгс/см2, тс/м2 ).
. Напряжение
имеет размерность интенсивности нагрузки, т.е. МПа (кгс/см2, тс/м2 ).
1 МПа=106Па=106Н/м2.
7.
Привести
формулы, связывающие внутренние силовые факторы с напряжениями.
Нормальные и касательные
напряжения в каждом поперечном сечении бруса связаны определенными
соотношениями с внутренними усилиями, действующими в этом сечении:
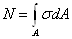
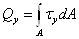
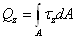
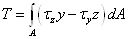
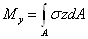
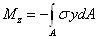
В формулах 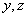 - координаты точки, в которой
определяются напряжения.
- координаты точки, в которой
определяются напряжения.
8.
Какой вид
деформации называется растяжением (сжатием) ?
Растяжением (сжатием)
называется такой вид деформации, когда в поперечном сечении стержня под
действием внешних нагрузок возникает только один внутренний силовой фактор –
продольная сила 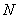 , а остальные внутренние силовые
факторы отсутствуют.
, а остальные внутренние силовые
факторы отсутствуют.
Продольная сила вызывает
нормальные 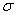 напряжения
, определяемые:
напряжения
, определяемые:
- при равномерном
распределении их по сечению 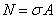
- при неравномерном
распределении 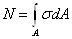
Продольная сила и
напряжение положительны при растяжении и отрицательны при сжатии.
9.
Абсолютная
и относительная деформация при растяжении (сжатии). Коэффициент Пуассона.
Если под действием силы 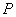 брус длиной
брус длиной 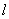 изменил свою
продольную величину на
изменил свою
продольную величину на 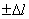 , то эта величина называется
абсолютной продольной деформацией (абсолютное удлинение или укорочение). При
этом наблюдается и поперечная абсолютная деформация
, то эта величина называется
абсолютной продольной деформацией (абсолютное удлинение или укорочение). При
этом наблюдается и поперечная абсолютная деформация 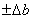 .
.
Отношение 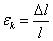 называется
относительной продольной деформацией, а отношение
называется
относительной продольной деформацией, а отношение 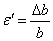 - относительной поперечной
деформацией.
- относительной поперечной
деформацией.
Отношение 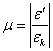 называется
коэффициентом Пуассона, который характеризует упругие свойства материала.
называется
коэффициентом Пуассона, который характеризует упругие свойства материала.
Коэффициент Пуассона
имеет значение 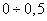 . (для стали он равен
. (для стали он равен 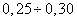 )
)
10.
Сформулировать
закон Гука при растяжении (сжатии).
I форма. В поперечных сечениях бруса
при центральном растяжении (сжатии) нормальные напряжения равны отношению
продольной силы к площади поперечного сечения:
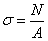
II форма. Относительная продольная
деформация прямо пропорциональна нормальному напряжению 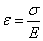 , откуда
, откуда 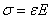 .
.
11.
Как
определяются напряжения в поперечных и наклонных сечениях бруса ?
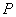 – сила, равная произведению
напряжения
– сила, равная произведению
напряжения 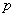 на
площадь наклонного сечения
на
площадь наклонного сечения 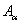 :
:
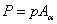
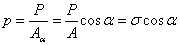
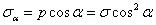
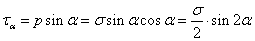
12.
По какой
формуле можно определить абсолютное удлинение (укорочение) бруса ?
Абсолютное удлинение
(укорочение) бруса (стержня) выражается формулой:
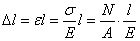 , т.е.
, т.е. 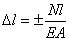
Учитывая, что величина 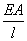 представляет
собой жесткость поперечного сечения бруса длиной
представляет
собой жесткость поперечного сечения бруса длиной 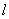 можно сделать вывод: абсолютная
продольная деформация прямо пропорциональна продольной силе и обратно
пропорциональна жесткости поперечного сечения. Этот закон впервые сформулировал
Гук в 1660 году.
можно сделать вывод: абсолютная
продольная деформация прямо пропорциональна продольной силе и обратно
пропорциональна жесткости поперечного сечения. Этот закон впервые сформулировал
Гук в 1660 году.
13.
Как
определяются температурные деформации и напряжения?
При повышении температуры
у большинства материалов механические характеристики прочности уменьшаются, а
при понижении температуры – увеличиваются. Например, у стали марки Ст3 при 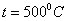
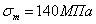 и
и 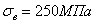 ;
;
при 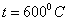
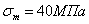 и
и 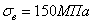 , т.е.
, т.е. 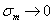 .
.
Удлинение стержня при
нагревании определяется по формуле 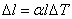 , где
, где 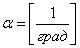 - коэффициент линейного
расширения материала стержня,
- коэффициент линейного
расширения материала стержня, 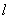 - длина стержня.
- длина стержня.
Возникающее в поперечном
сечении нормальное напряжение 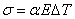 . При понижении температуры
происходит укорочение стержня и возникают напряжения сжатия.
. При понижении температуры
происходит укорочение стержня и возникают напряжения сжатия.
14.
Дать
характеристику диаграммы растяжения (сжатия).
Механические
характеристики материалов определяются путем испытаний образцов и построением
соответствующих графиков, диаграмм. Наиболее распространенным является
статическое испытание на растяжение (сжатие).
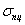 - предел пропорциональности (до
этого предела справедлив закон Гука);
- предел пропорциональности (до
этого предела справедлив закон Гука);
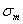 - предел текучести материала;
- предел текучести материала;
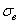 - предел прочности материала;
- предел прочности материала;
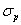 - разрушающее (условное)
напряжение;
- разрушающее (условное)
напряжение;
Точка 5 соответствует
истинному разрушающему напряжению.
1-2 площадка текучести
материала;
2-3 зона упрочнения
материала;
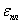 и
и 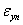 - величина пластической и упругой
деформации.
- величина пластической и упругой
деформации.
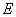 - модуль упругости при растяжении
(сжатии), определяемый как:
- модуль упругости при растяжении
(сжатии), определяемый как: 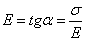 , т.е.
, т.е. 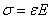 .
.
15.
Какие
параметры характеризуют степень пластичности материала ?
Степень пластичности
материала может быть охарактеризовано величинами:
- остаточным
относительным удлинением – как отношение остаточной деформации образца к
первоначальной его длине:
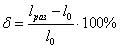
где 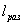 - длина образца после
разрыва. Величина
- длина образца после
разрыва. Величина 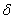 для различных марок стали
находится в пределах от 8 до 28 %;
для различных марок стали
находится в пределах от 8 до 28 %;
- остаточным
относительным сужением – как отношение площади поперечного сечения образца в
месте разрыва к первоначальной площади:
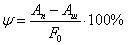
где 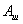 - площадь поперечного
сечения разорванного образца в наиболее тонком месте шейки. Величина
- площадь поперечного
сечения разорванного образца в наиболее тонком месте шейки. Величина 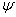 находится в
пределах от нескольких процентов для хрупкой высокоуглеродистой стали до 60 %
для малоуглеродистой стали.
находится в
пределах от нескольких процентов для хрупкой высокоуглеродистой стали до 60 %
для малоуглеродистой стали.
16.
Задачи,
решаемые при расчете на прочность при растяжении (сжатии).
Основное уравнение
прочности 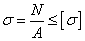
Задача 1. Проектный
расчет 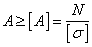
Задача 2. Проверочный
расчет 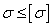
Задача 3. Определение
допускаемой нагрузки 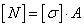
Задача 4. Условие
жесткости 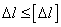
17.
Что
понимается под допускаемыми напряжениями ?
Для обеспечения
нормальной работоспособности детали необходимо, чтобы фактически возникающие
напряжения не превышали некоторого безопасного, или допускаемого напряжения,
обозначаемого 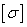 . Это такое напряжение, при
котором обеспечивается достаточная прочность и долговечность детали.
. Это такое напряжение, при
котором обеспечивается достаточная прочность и долговечность детали.
Допускаемое напряжение
определяется как 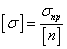 . В качестве предельного
напряжения
. В качестве предельного
напряжения 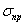 может
быть разрушающее напряжение
может
быть разрушающее напряжение 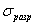 , предел текучести материала
, предел текучести материала 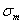 , предел
прочности
, предел
прочности 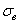 и
др.
и
др. 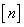 -
нормативный (требуемый) коэффициент запаса прочности или коэффициент
безопасности.
-
нормативный (требуемый) коэффициент запаса прочности или коэффициент
безопасности.
18.
Как
осуществляется решение статически неопределимых систем в сопротивлении
материалов ?
В теоретической механике
се тела считаются условно абсолютно твердыми. Задачи решаются с помощью обычных
уравнений равновесия (статики). В сопротивлении материалов все тела упругие,
под нагрузкой могут изменить форму и размер.
В статически
неопределимых системах внутренние усилия нельзя определить при помощи одних
уравнений равновесия. Необходимо составлять дополнительные уравнения (уравнения
совместности деформаций).
19.
Что
понимается в сопротивлении материалов под эпюрой ?
Эпюра – график,
показывающий изменение какого-либо параметра по длине конструкции. Например,
эпюра продольных сил по длине стержня, эпюра напряжений, эпюра деформаций,
эпюра поперечных сил при изгибе, эпюра изгибающих моментов и др.
Эпюры дают наглядное
представление о характере изменения силового фактора по длине или координате и
позволяют установить местонахождение опасных сечений.
20.
Сформулировать
основные гипотезы и допущения, принятые в сопротивлении материалов.
1)
Гипотеза о
сплошном строении тела.
2)
Гипотеза об
идеальной упругости материала.
3)
Гипотеза об
однородности материала.
4)
Гипотеза об
изотропности материала.
5)
Гипотеза плоских
сечений (Бернулли).
6)
Допущения о
малости деформаций.
7)
Допущения о
линейной зависимости между деформациями и нагрузками.
8)
Принцип
независимости действия сил (принцип суперпозиции).
9)
Принцип
Сен-Венана: в сечениях, достаточно удаленных от нагрузок, величина напряжений
весьма мало зависит от способа нагружения.
21.
Как
определяется удельная потенциальная энергия деформации при растяжении (сжатии)
?
Количество потенциальной
энергии, приходящейся на единицу объема бруса при растяжении (сжатии), т.е.
удельная потенциальная энергия деформации, определяется по формуле 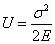 . Удельная
потенциальная энергия имеет размерность кгс·см/см3, тс·м/м3 и т.д.
. Удельная
потенциальная энергия имеет размерность кгс·см/см3, тс·м/м3 и т.д.
22.
Какое
напряженное состояние называется чистым сдвигом ?
Чистым сдвигом называют
такое напряженное состояние, когда на гранях выделенного из бруса элемента
действуют только касательные напряжения. Такие грани называются площадками
чистого сдвига.
Величина 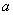 - абсолютный сдвиг,
- абсолютный сдвиг, 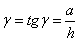 -
относительный сдвиг.
-
относительный сдвиг.
С деформацией сдвига мы
встречаемся при резании ножницами металла, при работе различных соединений
(резьбовых, шлицевых, шпоночных).
23.
Сформулировать
закон Гука для деформации сдвига.
Касательные напряжения 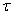 при сдвиге
прямо пропорциональны угловой деформации:
при сдвиге
прямо пропорциональны угловой деформации:
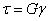 .
.
Коэффициент
пропорциональности 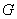 называется модулем сдвига или
модулем упругости второго рода. Модуль сдвига как и модуль упругости при
растяжении имеет размерность напряжений, т.е. МПа, кгс/см2.
называется модулем сдвига или
модулем упругости второго рода. Модуль сдвига как и модуль упругости при
растяжении имеет размерность напряжений, т.е. МПа, кгс/см2.
24.
Какой
зависимостью связаны основные механические характеристики материалов ?
Модули упругости первого
рода 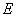 ,
второго рода
,
второго рода 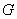 и коэффициент Пуассона
и коэффициент Пуассона 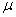 связаны
соотношением
связаны
соотношением 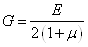 .
.
Учитывая, что 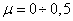 , можно
установить, что величина модуля сдвига
, можно
установить, что величина модуля сдвига 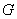 составляет от 0,33 до 0,5
величины модуля упругости
составляет от 0,33 до 0,5
величины модуля упругости 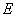 . Для большинства материалов можно
принимать
. Для большинства материалов можно
принимать 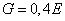 ,
следовательно, для стали
,
следовательно, для стали 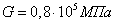 .
.
25.
Сформулировать
условие прочности при сдвиге и основные задачи, решаемые при этом.
Условие прочности при
сдвиге (срезе) имеет вид 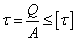 .
.
Допускаемое напряжение
при срезе обычно принимают как некоторую часть допускаемого напряжения
материала при растяжении. Для стали, меди, алюминия 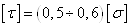 , для чугуна
, для чугуна 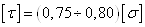 .
.
Задача 1. Проектный
расчет 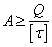 .
.
Задача 2. Проверочный
расчет 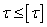 .
.
Задача 3. Определение
допускаемой силы 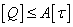 .
.
26.
Как
определяется полная удельная потенциальная энергия деформации тела при чистом
сдвиге ?
При чистом сдвиге
потенциальная энергия изменения объема равна нулю, а полная удельная
потенциальная энергия равна удельной потенциальной энергии изменения формы:
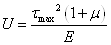 .
.
27.
Какой вид
деформации называется кручением ?
Кручением называется
такой вид деформации, при котором в поперечном сечении стержня под действием
внешних нагрузок возникает только один внутренний силовой фактор – крутящий
момент 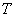 .
.
Крутящий момент вызывает
касательные напряжения 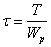 , где
, где 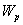 - полярный момент сопротивления
стержня.
- полярный момент сопротивления
стержня.
С крутящим моментом мы
сталкиваемся при расчете валов, при завинчивании болтов и др.
28.
Какая
зависимость существует между мощностью, приложенной к валу, крутящим моментом и
скоростью вращения вала ?
При расчете валов в ряде
случаев величины внешних скручивающих моментов определяются по величине
потребляемой мощности и по скорости вращения вала.
Из физики известно, что 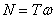 ,
, 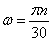 .
.
Тогда, если мощность
выражена в кгс·мc, 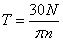 .
.
Если мощность 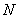 задана в
лошадиных силах, то
задана в
лошадиных силах, то 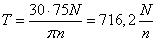 .
.
Если мощность задана в
киловаттах, то учитывая, что 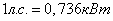 , получим
, получим
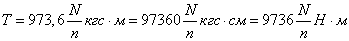 .
.
29.
Привести
пример построения эпюры крутящих моментов.
Каждая ордината эпюры
крутящих моментов в принятом масштабе равна величине крутящего момента,
действующего в том поперечном сечении бруса, которому соответствует эта
ордината. В сечении, в котором к брусу приложен внешний скручивающий момент,
ордината эпюры изменяется скачкообразно на величину этого момента.
Нужно иметь в виду, что
на прочность и жесткость знак крутящего момента не оказывает никакого значения.
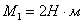 ;
; 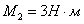 ;
; 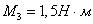 ;
; 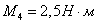 .
.
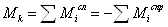 .
.
30.
Какие
существуют зависимости между деформациями сдвига и кручения ?
Установлено, что во всех
точках круглого бруса при кручении создается напряженное состояние чистого
сдвига, т.е. на всех гранях элементарного параллелепипеда, выделенного из
элемента бруса, нормальные напряжения отсутствуют.
В поперечных сечениях
бруса при кручении возникают касательные напряжения, направление которых в
каждой точке перпендикулярно к радиусу, а величина прямо пропорциональна
расстоянию точки от центра.
Величина этих напряжений,
на основании закона Гука при сдвиге, равна:
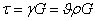 , где
, где 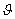 - относительный угол закручивания,
- относительный угол закручивания,
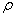 -
расстояние от точки до центра.
-
расстояние от точки до центра.
31.
По какой
формуле вычисляются касательные напряжения при кручении ?
Наибольшее касательное
напряжение, возникающее в непосредственной близости к наружной боковой
поверхности бруса, определится по формуле:
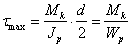 , где
, где 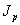 - полярный момент
инерции сечения,
- полярный момент
инерции сечения, 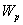 - полярный момент сопротивления
сечения.
- полярный момент сопротивления
сечения.
32.
Как
вычисляется угол закручивания вала при передаче крутящего момента ?
Если крутящий момент во всех
поперечных сечениях вала (бруса) имеет одно и то же значение, а размеры сечения
постоянны по всей его длине, то полный угол закручивания определиться по
формуле: 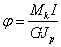
Произведение 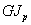 называется
жесткостью сечения при кручении. Оно выражается в кгс·мм2 , кгс·см2 и т.д.
называется
жесткостью сечения при кручении. Оно выражается в кгс·мм2 , кгс·см2 и т.д.
33.
Что
понимается под полярным моментом сопротивления ?
Полярным моментом
сопротивления сечения называется отношение полярного момента инерции к
расстоянию от центра тяжести сечения до наиболее удаленной его точки. Полярный
момент сопротивления выражается в см3 , мм3 и тд.
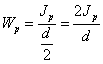 .
.
Для круглого сплошного
поперечного сечения 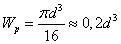 .
.
Для кольцевого сечения 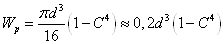 ,
, 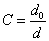 .
.
34.
Сформулировать
условие прочности при кручении и основные задачи, вытекающие из этого условия.
Условие прочности при
кручении запишется так: 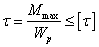 ,
, 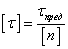 .
.
Задача 1. Подбор сечения
по заданной нагрузке 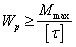 .
.
Задача 2. Проверка
действующих напряжений 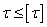 .
.
Задача 3. Определение
допускаемой нагрузки 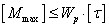 .
.
Задача 4. Условие
жесткости бруса 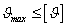 , где
, где 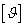 - допускаемый относительный угол
закручивания, принимаемый равным от 0,15 до 20 на 1м длины стержня.
- допускаемый относительный угол
закручивания, принимаемый равным от 0,15 до 20 на 1м длины стержня.
35.
Сформулировать
условие прочности винтовой цилиндрической пружины.
Такие пружины являются
одним из наиболее широко распространенных элементов современных механизмов и
машин. Сила 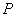 растяжения
пружины вызывает в сечении прутка касательные напряжения.
растяжения
пружины вызывает в сечении прутка касательные напряжения.
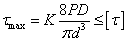 ,
,
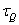 - касательные напряжения от
поперечной силы;
- касательные напряжения от
поперечной силы;
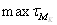 - касательные напряжения от
крутящего момента.
- касательные напряжения от
крутящего момента.
Коэффициент 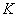 - поправочный,
определяемый как
- поправочный,
определяемый как 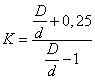 .
.
Жесткость пружины
вычисляется по формуле 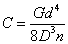 [ кгс/мм, кгс/см ], где
[ кгс/мм, кгс/см ], где 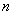 - число витков
пружин.
- число витков
пружин.
36.
Дать
определение основным видам изгиба.
Такой вид деформации,
когда в поперечных сечениях конструкции (стержня) возникают изгибающие моменты,
т.е. внутренние моменты, действующие в плоскости, перпендикулярной плоскости
поперечного сечения, называется изгибом.
Чистый изгиб – изгибающий
момент в сечении является единственным силовым фактором.
Поперечный изгиб – наряду
с изгибающим моментом в поперечном сечении возникают поперечные силы.
Прямой изгиб – если
плоскость действия изгибающего момента проходит через одну из главных
центральных осей инерции поперечного сечения.
Косой изгиб – если
плоскость действия изгибающего момента не проходит через одну из главных
центральных осей инерции поперечного сечения.
37.
Какие
внутренние силовые факторы возникают в сечении бруса при деформации изгиба ?
При действии на брус
внешних нагрузок, расположенных на одной плоскости, проходящей через ось бруса,
в каждом поперечном сечении возникают внутренние силовые факторы:
1)
продольная сила 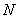 приложена в
центре тяжести сечения, действующая перпендикулярна к сечению;
приложена в
центре тяжести сечения, действующая перпендикулярна к сечению;
2)
поперечная сила 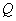 , действующая в
плоскости поперечного сечения, проходящая через его центр тяжести;
, действующая в
плоскости поперечного сечения, проходящая через его центр тяжести;
3)
изгибающий момент
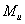 ,действующий
в плоскости, перпендикулярной к поперечному сечению.
,действующий
в плоскости, перпендикулярной к поперечному сечению.
38.
Как
определяется по величине и знаку поперечная сила в любом поперечном сечении
балки ?
Поперечная сила в любом
поперечном сечении балки равна сумме проекций всех действующих сил слева от
сечения на ось, перпендикулярную оси балки и сумме проекций всех сил справа от
сечения, но с обратным знаком.
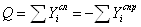 .
.
Поперечная сила имеет
положительное значение, если относительно сечения она стремится повернуть балку
по часовой стрелке (рис а), и отрицательное – если против часовой (рис б).
39.
Как
определяется в любом поперечном сечении балки изгибающий момент по величине и
знаку ?
Изгибающий момент в любом
сечении балки численно равен алгебраической сумме моментов, действующих на
балку внешних сил, относительно центра тяжести этого сечения.
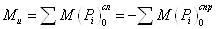 .
.
Изгибающий момент имеет
положительное значение, если он действует так, что ось балки изгибается
выпуклостью вниз (рис а) и отрицательное – выпуклостью вверх (рис б).
40.
Как
определяется в любом поперечном сечении балки продольная сила по величине и
знаку ?
Продольная сила 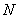 по величине и
знаку равна сумме проекций всех внешних сил, приложенных к левой части бруса,
на его продольную ось, или сумме проекций (на ту же ось), взятой с обратным
знаком, всех внешних сил, приложенных к правой части бруса :
по величине и
знаку равна сумме проекций всех внешних сил, приложенных к левой части бруса,
на его продольную ось, или сумме проекций (на ту же ось), взятой с обратным
знаком, всех внешних сил, приложенных к правой части бруса :
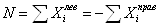 .
.
Продольная сила 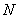 в сечении
положительна при растяжении и отрицательна при сжатии.
в сечении
положительна при растяжении и отрицательна при сжатии.
41.
Что
понимается под эпюрой внутренних усилий при изгибе ?
Закон изменения
внутренних усилий в поперечном сечении балки по ее длине можно выразить с
помощью специальных графиков, называемых эпюрами.
Эпюрой изгибающих
моментов (эпюрой 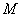 ) называется график, изображающий
закон изменения величин этих моментов по длине балки.
) называется график, изображающий
закон изменения величин этих моментов по длине балки.
Эпюрой поперечных сил
(эпюрой 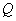 )
или эпюрой продольных сил (эпюрой
)
или эпюрой продольных сил (эпюрой 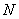 ) называется график, изображающий
изменение поперечных или продольных сил по длине балки.
) называется график, изображающий
изменение поперечных или продольных сил по длине балки.
42.
Привести
эпюру поперечных сил и изгибающих моментов для консольной балки, загруженной на
конце силой 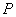 ?
?
В месте защемления 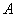 балки
возникают реактивный момент
балки
возникают реактивный момент 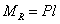 и опорная реакция
и опорная реакция 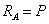 ; поперечная сила в
сечении
; поперечная сила в
сечении 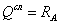 ,
,
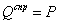 .
.
Изгибающий момент в
сечении 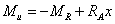 .
.
При 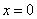
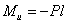 , при
, при 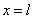
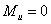 .
.
43.
Привести
дифференциальные зависимости между интенсивностью распределенной нагрузки,
поперечной силой и изгибающим моментом.
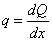 ,
, 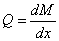 ,
, 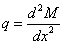 .
.
Интенсивность
распределенной нагрузки равна первой производной по абсциссе сечения от
поперечной силы или второй производной от изгибающего момента.
Поперечная сила в сечении
равна первой производной от изгибающего момента по абсциссе сечения (теорема
Д.И.Жуковского). Полученные зависимости используют при построении эпюр поперечных
сил и изгибающих моментов.
44.
Сформулировать
основные правила построения эпюр при изгибе .
1)
На участках
балки, на которых поперечная сила положительна, изгибающий момент возрастает
(слева направо), а на участках, на которых она отрицательна – убывает.
2)
Чем больше по
абсолютной величине значение поперечной силы 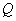 , тем круче линия, ограничивающая
эпюру
, тем круче линия, ограничивающая
эпюру 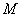 .
.
3)
На участке балки,
на котором поперечная сила имеет постоянное значение, эпюра 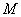 ограничена прямой
линией.
ограничена прямой
линией.
4)
Если на границе
соседних участков балки эпюра 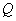 не имеет скачка, то линии,
ограничивающие эпюру
не имеет скачка, то линии,
ограничивающие эпюру 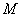 на этих участках, сопрягаются без
перелома, т.е имеют в точке общую касательную.
на этих участках, сопрягаются без
перелома, т.е имеют в точке общую касательную.
5)
Если на границе
соседних участков балки в эпюре 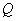 имеется скачок, то линии,
ограничивающие эпюру
имеется скачок, то линии,
ограничивающие эпюру 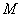 на этих участках, сопрягаются с
переломом.
на этих участках, сопрягаются с
переломом.
6)
Изгибающий момент
достигает максимума или минимума в сечениях балки, в которых поперечная сила
равна нулю; касательная к линии, ограничивающей эпюру 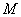 , в этом сечении параллельна оси
эпюр.
, в этом сечении параллельна оси
эпюр.
7)
На участках
действия распределенной нагрузки поперечные силы изменяются по длине балки
(если интенсивность 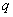 постоянна, то поперечные силы
изменяются по линейному закону).
постоянна, то поперечные силы
изменяются по линейному закону).
8)
На участках
балки, на которых распределенная нагрузка отсутствует, поперечные силы
постоянны, а изгибающие моменты меняются по линейному закону.
45.
Как
определяются напряжения при изгибе ?
По закону Гука 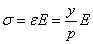 нормальное
напряжение в поперечном сечении прямо пропорционально расстоянию от
рассматриваемой точки до нейтральной оси n-n.
нормальное
напряжение в поперечном сечении прямо пропорционально расстоянию от
рассматриваемой точки до нейтральной оси n-n.
При 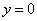
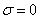 , при
, при 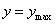
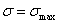 .
.
46.
Сформулировать
условие прочности при изгибе и основные задачи, вытекающие из этого условия.
Основное уравнение 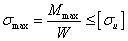 .
.
Задача 1. Проектная 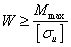 .
.
Задача 2. Проверочная 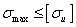 .
.
Задача 3. Определение
допускаемой нагрузки 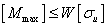 .
.
47.
Что
понимается под моментом сопротивления при изгибе ?
При поперечном сечении,
симметричном относительно нейтральной оси, абсолютные величины наибольших
растягивающих и сжимающих напряжений одинаковы и определяются по формуле 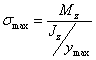 .
.
Величина 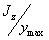 , зависящая только от
размеров и формы поперечного сечения, называется осевым моментом сопротивления
, зависящая только от
размеров и формы поперечного сечения, называется осевым моментом сопротивления
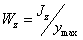 .
.
Для прямоугольного
сечения шириной 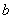 и высотой
и высотой 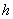 :
: 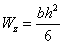 .
.
Для круглого сечения
диаметром 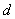 :
:
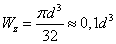 .
.
48.
Сформулировать
основное дифференциальное уравнение упругой линии при изгибе.
Уравнение имеет вид 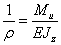 .
.
Величина 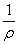 представляет собой
кривизну изогнутой оси балки и характеризует величину деформации при изгибе.
представляет собой
кривизну изогнутой оси балки и характеризует величину деформации при изгибе.
Величина 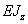 - произведение модуля
упругости на момент инерции сечения, характеризует жесткость сечения при
изгибе.
- произведение модуля
упругости на момент инерции сечения, характеризует жесткость сечения при
изгибе.
Вывод: величина
деформации изогнутой оси балки прямо пропорциональна изгибающему моменту 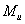 и обратно
пропорциональна жесткости при изгибе
и обратно
пропорциональна жесткости при изгибе 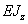 .
.
Принимая из математики,
что 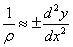 ,
получим
,
получим 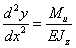 .
.
49.
Привести
уравнение углов поворота сечения балки и уравнение прогибов при изгибе.
После двойного
интегрирования основного дифференциального уравнения 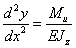 получаем уравнение углов поворота
сечений
получаем уравнение углов поворота
сечений 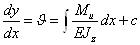
и уравнение прогибов 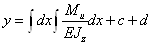 .
.
Постоянные интегрирования
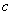 и
и 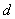 определяются
по начальным условиям (условия закрепления балки).
определяются
по начальным условиям (условия закрепления балки).
50.
Назвать
геометрические характеристики плоских сечений и их размерности.
При расчетах элементов
конструкций используются различные геометрические характеристики, а именно:
1)
Площадь
поперечного сечения (см2, мм2).
2)
Статические
моменты сечения (см3, мм3).
3)
Осевые моменты
инерции сечения (см4, мм4).
4)
Полярные моменты
инерции сечения (см4, мм4).
5)
Центробежные
моменты инерции (см4, мм4).
6)
Осевые и полярные
моменты сопротивления сечения (см3, мм3).
51.
Назвать
простейшую геометрическую характеристику поперечного сечения.
Самой простой геометрической
характеристикой поперечного сечения является площадь. При расчетах на
растяжение (сжатие), сдвиг, устойчивость именно она определяет уровень
напряжений.
Если представить сечение
состоящим из множества элементарных площадок, то площадь всего сечения 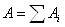 или
или 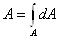 .
.
52.
Что
понимается под моментом инерции сечения ?
Осевым моментом инерции
сечения относительно некоторой оси называется взятая п всей его площади сумма
произведений элементарных площадок на квадраты их расстояний от этой оси, т.е. 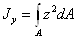 ,
, 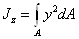 .
.
Полярным моментом инерции
сечения относительно некоторой точки (полюса) называется 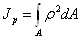 , где
, где 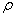 - расстояние от сечения
до полюса.
- расстояние от сечения
до полюса.
Очевидно, что 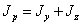 .
.
Центробежным моментом
инерции сечения относительно двух взаимно перпендикулярных осей называется 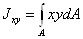 .
.
53.
В каком
случае центробежный момент инерции сечения равен нулю ?
Центробежные моменты
инерции сечения могут быть положительными, отрицательными или равными нулю в
зависимости от координат 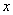 и
и 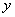 .
.
Центробежный момент
инерции сечения относительно осей, одна из которых или обе совпадают с его
осями симметрии, равен нулю.
Оси, относительно которых
центробежный момент инерции сечения равен нулю, называются главными.
54.
Привести
формулы геометрических характеристик для прямоугольного сечения.
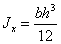 ,
, 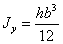 ,
, 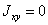 ;
;
 ,
,  ,
, 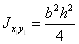 ;
;
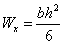 ,
, 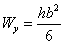 .
.
55.
Привести
формулы геометрических характеристик для сплошного круглого сечения.
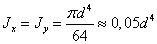 ,
, 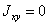 ;
;
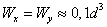 ;
;
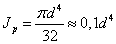 ;
;
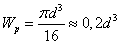 .
.
56.
Привести
формулы геометрических характеристик для кольцевого сечения.
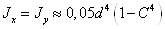 ;
;
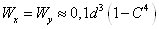 ;
;
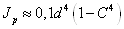 ;
;
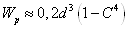 , где
, где 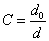 .
.
57.
Привести
формулы геометрических характеристик для треугольника.
 ,
, 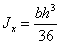 ,
, 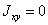 (рис а);
(рис а);
 ,
, 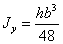 ,
, 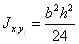 ,
, 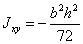 (рис б).
(рис б).
58.
Привести
формулы, описывающие моменты инерции сечений, относительно параллельных осей.
Осевые моменты инерции
сечений относительно новых осей 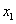 и
и 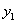 :
:
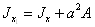 ,
, 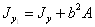 .
.
Центробежные моменты
инерции сечений
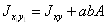 ,
,
где 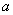 и
и 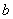 - смещение новых осей
относительно старых, причем старые оси должны проходить через центр тяжести
сечения.
- смещение новых осей
относительно старых, причем старые оси должны проходить через центр тяжести
сечения.
59.
Как
определяются моменты инерции сечений при повороте осей ?
Если проведем оси 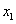 и
и 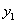 , повернутые
относительно старых на угол
, повернутые
относительно старых на угол 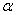 , то моменты инерции определяются
по формулам:
, то моменты инерции определяются
по формулам:
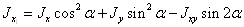 ,
,
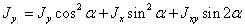 .
.
Очевидно, что 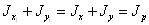 .
.
Центробежный момент
инерции сечения 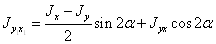 .
.
При повороте осей на 900
очевидно, что
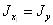 ,
, 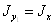 ,
, 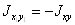 .
.
60.
Что
понимается под главными осями инерции сечения и как определяется их положение ?
Взаимно перпендикулярные
оси, из которых одна или обе совпадают с осями симметрии сечения, всегда
являются главными осями инерции.
Оси, относительно которых
осевые моменты инерции имеют экстремальные значения, называются главными осями
инерции.
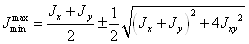 .
.
Относительно главных осей
инерции центробежный момент инерции равен нулю.
Положение главных осей
инерции определяется углом 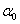 :
:
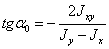 .
.
61.
Что
понимается под радиусами инерции сечения ?
Радиусом инерции сечения
относительно некоторой оси, например 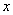 , называется величина
, называется величина 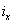 , определяемая
из равенства
, определяемая
из равенства
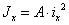 , откуда
, откуда 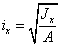 .
.
Радиусы инерции,
соответствующие главным осям, называются главными радиусами инерции.
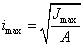 ,
, 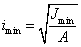 .
.
62.
Сформулировать
основные виды напряженного состояния конструкции.
Совокупность нормальных и
касательных напряжений, действующих по всем площадкам, проходящим через
рассматриваемую точку, называется напряженным состоянием в этой точке.
При объемном (трехосном)
напряженном состоянии (рис а) нет площадок, в которых нормальные и касательные
напряжения были бы равны.
При плоском (двухосном)
напряженном состоянии (рис б) в одной из площадок касательные и нормальные
напряжения равны нулю.
При линейном (одноосном)
напряженном состоянии (рис в) касательные и нормальные напряжения равны нулю в
двух площадках, проходящих через рассматриваемую точку.
63.
Назвать
основные теории прочности, по которым оценивается напряженное состояние
материала.
Теории прочности
представляют собой гипотезы о критериях, определяющих условия перехода
материала в опасное состояние.
Первая теория прочности
представляет собой гипотезу о том, что опасное состояние материала наступает,
когда наибольшее растягивающее напряжение достигает опасного значения.
Вторая теория прочности
представляет собой гипотезу, согласно которой опасное состояние материала
наступает в результате того, что наибольшее относительное удлинение достигает
опасного значения.
Третья теория прочности
представляет собой гипотезу, согласно которой опасное состояние материала
наступает, когда наибольшие касательные напряжения в нем достигают опасного
значения.
Четвертая
(энергетическая) теория прочности представляет собой гипотезу о том, что
причиной возникновения опасного состояния является величина удельной потенциальной
энергии изменения формы.
Теория прочности Мора –
можно считать, что прочность материала определяется лишь наибольшим и
наименьшим главными напряжениями.
Расчет трехосного
состояния сводится к расчету прочности при двухосном напряженном состоянии
построением кругов Мора.
Единая теория прочности
объясняет разрушение материала как в результате отрыва, так и сдвига, и может
использоваться при любом виде напряженного состояния.
64.
Что
понимается под сложным сопротивлением ?
К сложному сопротивлению
относятся виды деформаций бруса, при которых в его поперечных сечениях
одновременно возникают не менее двух внутренних силовых факторов.
Рассматриваются следующие
виды сложного сопротивления: косой изгиб, внецентренное растяжение и сжатие,
изгиб с кручением, сжатие с кручением, сжатие (растяжение) с изгибом и
кручением.
Сложное сопротивление
может быть получено путем суммирования напряженных состояний, вызванных каждым
отдельным видом простого нагружения.
65.
Как
определяются напряжения при внецентренном растяжении (сжатии) ?
Если на жесткий брус в
его верхнем поперечном сечении одновременно действуют продольная сила 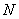 и изгибающие
моменты
и изгибающие
моменты 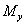 и
и
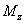 , то
нормальное напряжение в произвольной точке равно сумме напряжений
, то
нормальное напряжение в произвольной точке равно сумме напряжений
 .
.
Формулу можно
использовать, если сила 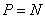 приложена не по центру, а,
например, в точке
приложена не по центру, а,
например, в точке 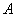 со смещением
со смещением 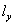 и
и 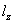 .
.
66.
Как
определяются напряжения при косом изгибе ?
Косой изгиб можно
рассматривать как сочетание двух прямых изгибов, вызванных изгибающими
моментами относительно главных центральных осей инерции поперечного сечения.
Напряжение в любой точке
определяется как 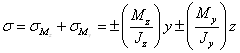 .
.
67.
Как
определяется приведенный (эквивалентный) момент по третьей и четвертой теориям
прочности ?
По третьей теории
прочности 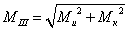 .
.
По четвертой теории
прочности 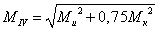 ,
где
,
где 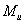 -
изгибающий момент,
-
изгибающий момент, 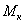 - крутящий момент.
- крутящий момент.
68.
По какой формуле
можно определить предварительный диаметр вала, работающего на кручение ?
Валы обычного работают на
кручение с изгибом. Предварительный диаметр вала с учетом только кручения
определяют из условия прочности по заниженным допускаемым напряжениям
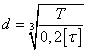
после этого разрабатывают
схему нагружения вала и уточняют диаметр вала по приведенному моменту.
69.
Как определяются
напряжения по третьей и четвертой теориям прочности при изгибе с кручением ?
По третьей теории
прочности 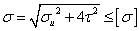 .
.
По четвертой теории
прочности 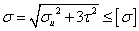 .
.
Соответственно условия
прочности имеют вид:
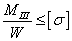 ,
, 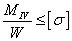 .
.
70.
Какова
последовательность расчета вала, работающего на изгиб с кручением?
Сочетание изгиба и
кручения брусьев круглого поперечного сечения наиболее часто рассматривается
при расчете валов. Последовательность расчета может быть следующей:
1)
Выполняется
расчетная схема вала.
2)
Определяются
внешние нагрузки.
3)
Определяются
опорные реакции в горизонтальной и вертикальной плоскостях.
4)
Строятся эпюры
изгибающих моментов в горизонтальной и вертикальной плоскости.
5)
Строится эпюра
суммарного изгибающего момента.
6)
Строится эпюра
крутящих моментов.
7)
Определяется
приведенный момент по одной из теорий прочности.
8)
Определяются
действующие напряжения и сравниваются с допускаемыми.
9)
Определяется
диаметр вала только по условию кручения и по условию кручения с изгибом и
выбирается наибольший.
71.
Что
понимается под устойчивым состоянием упругого тела ?
Из механики известно, что
равновесие твердых тел может быть устойчивым и неустойчивым.
При устойчивом равновесии
тело, выведенное какой-либо внешней силой из положения равновесия, возвращается
в это положение после прекращения действия силы. Аналогичная картина
наблюдается в статике упругих тел.
Устойчивость или
неустойчивость формы равновесия упругого тела зависит от его размеров,
материала, величин и направления сил.
72.
Что
понимается под критическим состоянием равновесия упругого тела ?
Значение силы, нагрузки и
напряжения, при которых первоначальная форма равновесия упругого тела
становится неустойчивой, называется соответственно критической силой,
критической нагрузкой и критическим напряжением.
Понятие устойчивости не
следует смешивать с понятием прочности; каждое из них имеет самостоятельное
значение. Потеря устойчивости не всегда связана с потерей прочности.
73.
Привести
формулу критической силы для центрального сжатого прямого стержня.
Формула была впервые
получена Эйлером и носит название эйлеровой критической силы
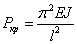 .
.
Если сжимающая сила
меньше критической, то возможна только прямолинейная форма равновесия, которая
в этом случае является устойчивой.
Приведенная формула дает
значение критической силы для стержня с шарнирно закрепленными концами.
74.
Как влияет
способ закрепления стержня на величину критической силы ?
Формулу Эйлера для
определения критической силы при различных закреплениях концов стержня можно
записать как 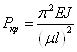 .
.
Коэффициент 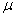 позволяет любой
случай закрепления концов стержня свести к основному случаю – к стержню с
шарнирно закрепленными концами.
позволяет любой
случай закрепления концов стержня свести к основному случаю – к стержню с
шарнирно закрепленными концами.
Для шарнирно закрепленных
концов 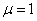 ;
;
Для стержня с
закрепленными концами 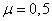 ;
;
Для стержня с одним
закрепленным и другим свободным концом 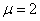 ;
;
Для стержня с одним
заделанным и другим шарнирно закрепленным концом 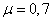 .
.
75.
По какой
формуле вычисляется критическое напряжение ?
Критическое сжимающее
напряжение, т.е. такое, при котором прямолинейная форма равновесия стержня
становится неустойчивой, определится по формуле
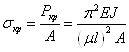 .
.
Введем понятие гибкости
стержня 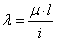 ,
получим
,
получим 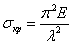 ,
где
,
где 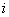 -
радиус инерции поперечного сечения стержня.
-
радиус инерции поперечного сечения стержня.
76.
Что
понимается под гибкостью стержня ?
Безразмерная величина 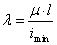 носит название
гибкости стержня и характеризует его способность сопротивляться искривлению в
зависимости от размеров и способа закрепления концов.
носит название
гибкости стержня и характеризует его способность сопротивляться искривлению в
зависимости от размеров и способа закрепления концов.
Предельная гибкость 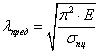 , при которой
формула Эйлера еще применима. Например, для стали Ст3
, при которой
формула Эйлера еще применима. Например, для стали Ст3 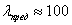 , при
, при 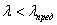 нужно пользоваться формулой
Ясинского.
нужно пользоваться формулой
Ясинского.
77.
Определить
область применимости формулы Эйлера при расчетах на устойчивость.
Приведенная формула
Эйлера справедлива тогда, когда напряжение 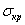 в материале, вызванное
критической силой , не превышает предела пропорциональности, т.е.
в материале, вызванное
критической силой , не превышает предела пропорциональности, т.е. 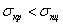 . Формулой
Эйлера можно пользоваться лишь в пределах применимости закона Гука
. Формулой
Эйлера можно пользоваться лишь в пределах применимости закона Гука
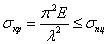 .
.
Отсюда получим формулу
для предельной гибкости 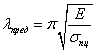 .
.
Условие применимости
формулы Эйлера можно представить в виде 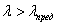 .
.
78.
Как
определяются критические напряжения при гибкости стержня меньше предельной ?
Действительные
критические силы и критические напряжения для стержней, гибкость которых ниже
предельной, значительно меньше величин, определяемых по формуле Эйлера. Для
таких стержней критические напряжения рекомендуется определять по эмпирическим
формулам Ф.С. Ясинского:
для стали 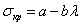 ;
;
для чугуна 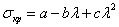 , где
, где 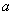 ,
,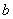 и
и 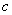 - определяемые
экспериментально коэффициенты, зависящие от свойств материала.
- определяемые
экспериментально коэффициенты, зависящие от свойств материала.
Например, для Ст3 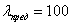 ,
, 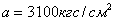 ,
, 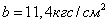 ,
, 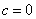 ;
;
Для дерева (сосна) 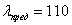 ,
, 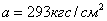 ,
, 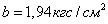 .
.
79.
Привести
графическую зависимость между критическими напряжениями и гибкостью стержня из
углеродистой стали Ст3.
Участок I соответствует простому сжатию
коротких стержней, II – напряжению,
определяемому по формуле Ясинского, III – напряжению, определяемому по формуле Эйлера, когда 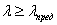 .
.
80.
Записать
условие устойчивости стержня через допускаемое напряжение 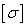 .
.
Допускаемое напряжение 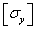 через
допускаемое напряжение на прочность
через
допускаемое напряжение на прочность 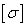 запишется так :
запишется так : 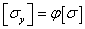 , где
, где 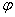 - коэффициент уменьшения
основного допускаемого напряжения для сжатых стержней, который зависит от
материала стержня и его гибкости.
- коэффициент уменьшения
основного допускаемого напряжения для сжатых стержней, который зависит от
материала стержня и его гибкости.
Тогда условие
устойчивости выражается неравенством 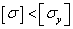 .
.
Кроме условия
устойчивости сжатые стержни должны удовлетворять и условию прочности 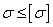 .
.
81.
Какие
задачи можно решать при расчетах на устойчивость ?
В основном
рассматриваются два вида расчетов:
1) проверочный, 2)
проектировочный.
При проверочном расчете
определяются критические напряжения и уточняется Коэффициент запаса
устойчивости 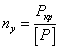 .
.
При проектировочном
расчете осуществляется подбор рационального сечения, используя геометрические
характеристики сечений, а именно площадь поперечного сечения 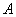 , осевые моменты инерции
, осевые моменты инерции
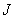 , радиусы
инерции
, радиусы
инерции 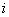 .
.
82.
Что
понимается под местными напряжениями ?
Напряжения, возникающие
при взаимном нажатии двух соприкасающихся тел, называются местными или
контактными. Вследствие деформации материала в месте соприкосновения возникает
площадка контакта, по которой и происходит передача давления. Контактные
напряжения весьма быстро убывают по мере удаления от места соприкосновения.
83.
Привести
примеры деталей, в которых могут возникать контактные напряжения.
Контактные напряжения
играют основную роль при расчете шариковых и роликовых подшипников, зубчатых
колес, элементов кулачковых механизмов, колес подвижного состава, шаровых и
цилиндрических катков и др.
Нагрузка у таких деталей
передается через малые участки поверхности и вызывает в зоне контакта большие
контактные напряжения.
84.
Дать
характеристику контактного взаимодействия двух шаров.
При сжатии двух шаров
радиусами 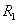 и
и
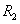 силой
силой 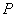 в результате
местных упругих деформаций образуется площадка контакта диаметром
в результате
местных упругих деформаций образуется площадка контакта диаметром 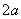 .
.
Радиус этой площадки 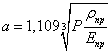 .
.
Напряжение в центре
площадки 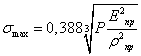 ,
где
,
где 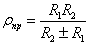 ,
, 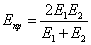 .
.
85.
Дать
характеристику контактного взаимодействия двух цилиндров.
При сжатии двух цилиндров
радиусами 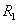 и
и
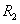 и
длиной
и
длиной 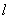 нагрузкой
интенсивностью
нагрузкой
интенсивностью 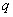 площадка контакта имеет вид
полоски шириной
площадка контакта имеет вид
полоски шириной 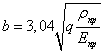 и длиной
и длиной 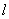 .
.
Наибольшее напряжение для
материалов с 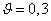 будет равно
будет равно 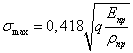 .
.
86.
Как
распределяются касательные напряжения при контактных нагрузках ?
Наибольшее касательное
напряжение возникает под поверхностью площади контакта на глубине примерно 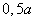 при круговой
площадке и
при круговой
площадке и 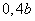 при
площадке в виде полоски. Значение максимального касательного напряжения
при
площадке в виде полоски. Значение максимального касательного напряжения 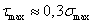 .
.
Наибольшее касательное
напряжение на площадке контакта в форме круга действует на контуре площадки, а
на площадке в форме полоски действует посредине полоски.
87.
Что
понимается под усталостью материала ?
Процесс постепенного
накопления повреждений материала при действии повторно-переменных напряжений,
приводящий к образованию трещин и разрушению, называется усталостью материала.
Известна некоторая
неизбежная неоднородность структуры металла, в связи с чем в окрестностях
отдельных точек материал обладает пониженной прочностью. При действии
переменных напряжений в окрестностях этих точек возникают микроскопические
трещины (как концентраторы напряжений), которые, развиваясь, уменьшают рабочую
площадь сечений, и происходит разрушение элемента.
88.
Что
понимается под выносливостью материала ?
Способность материала
воспринимать многократное действие переменных напряжений называют выносливостью,
а проверку прочности элементов конструкции при действии таких напряжений –
расчетом на выносливость (расчетом на усталостную прочность).
Наибольшее напряжение
цикла, при котором не происходит усталостного разрушения образца из данного
материала после произвольно большого числа циклов, называют пределом
выносливости.
89.
Назвать
основные параметры цикла переменных напряжений.
1)
Максимальные и
минимальные напряжения цикла 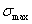 и
и 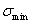 .
.
2)
Средние
напряжения цикла 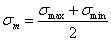 .
.
3)
Амплитудные
напряжения цикла 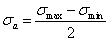 .
.
4)
Коэффициент
асимметрии цикла 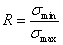 .
.
5)
Характеристика
цикла 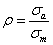 или
или
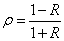 .
.
90.
Назвать
характерные циклы изменения напряжений.
Для симметричного цикла
(рис а) 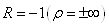 ,
знакопеременные циклы (рис б) могут иметь
,
знакопеременные циклы (рис б) могут иметь 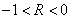 и
и 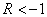 , знакопостоянные циклы (рис в)
могут иметь
, знакопостоянные циклы (рис в)
могут иметь 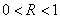 и
и
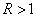 , для
отнулевого цикла (рис г) при положительных значениях напряжений
, для
отнулевого цикла (рис г) при положительных значениях напряжений 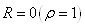 , а при отрицательных -
, а при отрицательных - 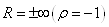 .
.
91.
Что
представляет собой кривая выносливости Велера ?
Для получения
механических характеристик, необходимых для расчетов при переменных
напряжениях, проводят специальные испытания на выносливость. Испытывая
специальные образцы (не менее 10 штук), строят графики зависимости напряжений
от числа циклов нагружения.
Кривая выносливости
показывает, что с увеличением числа циклов уменьшается максимальное напряжение,
при котором происходит разрушение материала.
Кривые выносливости могут
быть построены в координатах 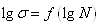 для более точного определения
предела выносливости.
для более точного определения
предела выносливости.
92.
Назвать
основные факторы, влияющие на величину предела выносливости.
Влияние факторов, от
которых зависит соотношение между пределами выносливости материала и детали,
более полно изучено лишь для симметричного цикла изменения напряжений.
1)
Снижение предела
выносливости за счет наличия тех или иных концентраторов напряжений учитывается
эффективным или действительным коэффициентом концентрации напряжений 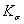 .
.
2)
Снижение предела
выносливости с ростом абсолютных размеров детали носит название масштабного
эффекта и учитывается масштабным коэффициентом 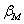 .
.
3)
Состояние
поверхностного слоя материала детали оказывает существенное влияние на
прочность при переменных напряжениях. Риски от механической обработки,
повреждения и т.п. играют роль концентраторов напряжений и ведут к снижению
предела выносливости. Этот фактор учитывается коэффициентом качества поверхности
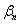 .
.
93.
Какая
зависимость существует между теоретическим и эффективным коэффициентом
концентрации напряжений ?
Местное повышение
напряжений, снижающее предел выносливости по сравнению с гладкими образцами,
учитывается эффективным коэффициентом концентрации напряжений 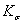 , который определяется
экспериментальным путем.
, который определяется
экспериментальным путем.
С теоретическим
коэффициентом концентрации коэффициент 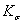 связан соотношением
связан соотношением
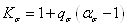 , где
, где 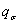 - коэффициент чувствительности
материала к концентрации.
- коэффициент чувствительности
материала к концентрации.
94.
Как
определить коэффициенты запаса прочности по усталостному разрушению ?
В расчетной практике
принято коэффициент снижения предела выносливости относить только к амплитудным
напряжениям цикла.
Тогда коэффициенты запаса
прочности по усталостному разрушению будут иметь вид:
- при изгибе  ;
;
- при кручении  .
.
Общий коэффициент запаса
прочности : 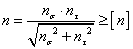 .
.
95.
Как
определяется общий коэффициент снижения предела выносливости при симметричном
цикле изменения напряжений ?
Совместное влияние
коэффициента концентрации напряжений, масштабного эффекта и состояния
поверхности оценивают общим коэффициентом снижения предела выносливости при
симметричном цикле:
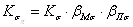 ,
, 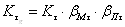 .
.
96.
Дать
характеристику динамическим нагрузкам, действующим на конструкцию.
Статической называется
нагрузка, которая весьма медленно возрастает от нуля до своего конечного
значения. Ускорения частиц элементов конструкции от такой нагрузки невелики, а
поэтому силами инерции можно пренебречь. При быстро возрастающей нагрузке
необходимо учитывать силы инерции, возникающие в результате деформации системы;
также нужно учитывать силы инерции от нагрузки, вызывающей ускоренное движение
тела.
Такие нагрузки,
напряжения и деформации называются динамическими. К динамическим также
относятся ударные нагрузки.
Расчет на действие
динамической нагрузки производится при проектировании частей конструкции,
находящихся под действием ударной или вибрационной нагрузки, вызванной
работающими стенками, двигателями, молотами и другими механизмами.
97.
Сформулировать
принцип Даламбера для динамической системы.
Из теоретической механики
известен принцип Даламбера, согласно которому движущееся тело или систему тел
можно рассматривать находящимися в равновесии, если приложить силы инерции.
Силы инерции выступают как дополнительная внешняя нагрузка на упругую систему.
Расчет конструкций с
учетом сил инерции и возникающего движения масс системы называют динамическим
расчетом.
98.
Явление
удара и деформация системы при ударе.
При падении груза 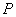 с высоты
с высоты 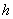 на какую-либо
неподвижно закрепленную упругую систему наблюдается явление удара. При этом предполагается,
что удар является неупругим, т.е. ударяющееся тело не отскакивает от
конструкции, а перемещается вместе с ней.
на какую-либо
неподвижно закрепленную упругую систему наблюдается явление удара. При этом предполагается,
что удар является неупругим, т.е. ударяющееся тело не отскакивает от
конструкции, а перемещается вместе с ней.
Целью расчета на удар
является определение наибольших деформаций и напряжений, возникающих в
результате удара.
99.
Что
понимается под коэффициентом динамичности ?
1)
При ударе
падающего груза на балку 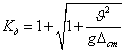 ;
;
2)
При вертикальном
ударе груза по телу 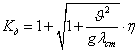 , где
, где 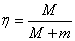 -учитывает соотношение ударяемой
-учитывает соотношение ударяемой 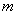 и ударяющей
и ударяющей 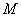 масс,
масс, 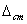 и
и 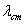 - статический
прогиб и статическое перемещение.
- статический
прогиб и статическое перемещение.
Зная коэффициент динамичности,
можно определить динамические напряжения 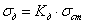 .
.
Как
определяется коэффициент динамичности при действии на систему возмущающей силы
?
При колебаниях системы
под действием возмущающей силы динамический коэффициент определяется по
формуле:
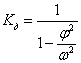 , где
, где 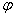 - круговая частота возмущающей
силы,
- круговая частота возмущающей
силы, 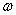 -
круговая частота свободных колебаний,
-
круговая частота свободных колебаний, 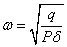 , где
, где 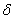 - прогиб балки под грузом от силы
- прогиб балки под грузом от силы 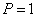 .
.
Для определения
динамических напряжений в упругой среде следует найти напряжения от статически
действующей силы и умножить на 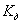 .
.