Контрольная работа: Расчет тока в линейных проводах и разветвленной цепи

Задача 1. Расчет разветвленной цепи постоянного тока с одним источником энергии

Условие задачи. В электрической цепи, изображенной на рисунке, определить токи в ветвях, напряжение на зажимах и составить баланс мощности. Значения сопротивлений резисторов и ток в ветви с сопротивлением r2.

I2 = 12A; r1 = 8Ом; r2 = 7Ом; r3 = 9Ом; r4 = 7Ом; r5 = 6Ом; r6 = 15Ом.

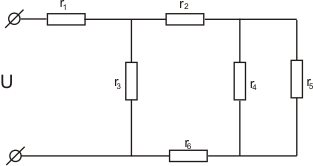
Решение:

Преобразуем цепь к эквивалентной.

Сопротивления r4 и r5 соединены параллельно, поэтому их можно заменить сопротивлением

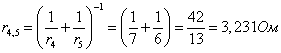
Схеме будет иметь вид:

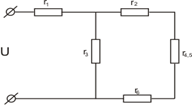
Сопротивления r2 , r4,5 и r6 соединены последовательно. Следовательно их можно заменить сопротивлением

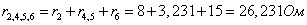
Схема будет иметь вид:

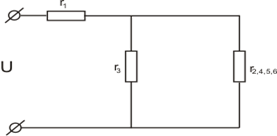
Сопротивления r3 и r2,4,5,6 соединены параллельно, поэтому заменяем их сопротивлением :

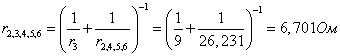
Схема имеет вид:

Сопротивления и соединены последовательно, поэтому общее сопротивление цепи:

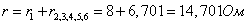
Эквивалентная схема:

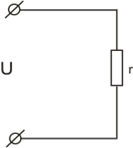
Ток в ветви с r2 известен, соответственно, ток через сопротивления r4,5 и r6 такой же, т.к. эти элементы соединены последовательно. Поэтому I6 = I2 = 12A. Падение напряжения на этих сопротивлениях (по закону Ома ):

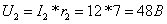
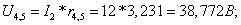
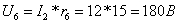
Токи через сопротивления r4 и r5 :

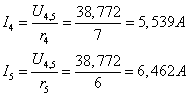
Т.к. r3 и r2,4,5,6 соединены параллельно, то падение напряжения на r3 такое же, как и на r2,4,5,6.

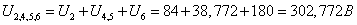
Ток через сопротивление r3;

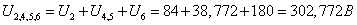
Т.к. U2,3,4,5,6 = U3 = U2,4,5,6 , то ток через сопротивление r2,3,4,5,6 равен:

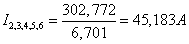
Т.к. r1 и r2,3,4,5,6 соединены последовательно, то

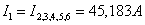
Следовательно напряжение на зажимах:

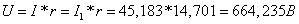
Составляем баланс мощности:

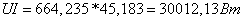
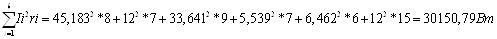
Различия получившихся значений составляет:

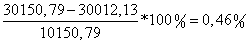 , что вызвано ошибками округления.

Следовательно, в пределах ошибок вычислений, полученные величины совпадают

Ответ: I1 = 45,183A ; I2 = 12A ; I3 = 33,641A ; I4 = 5,539A ; I5 = 6,462A; I6 = 12A ; U =664,235B

Задача 2. Расчет разветвленной цепи постоянного тока с несколькими источниками энергии

Условие задачи. Для разветвленной электрической цепи, требуется:

– на основе законов Кирхгофа составить уравнения для определения токов (решать систему уравнений не следует);

– определить токи в ветвях схемы методом контурных токов;

– определить режимы работы активных ветвей и составить баланс мощностей.

Е1 = 70В; Е2 = 190В; r1 = 1Ом; r2 = 4Ом; r3 = 25Ом; r4 = 18Ом; r5 = 24ОМ; r6 = 22Ом.

Решение:

1)  укажем направления токов во всех ветвях схемы. Контуры I, II и III будем обходить по часовой стрелке.

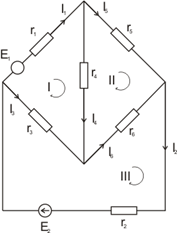
В данной схеме 4 узла; 6 ветвей. Следовательно, по 1-му закону Кирхгофа можно составить 6 – 4 + 1 =3 ур-я. Имеем:

I1 – I4 – I5 = 0

I3 + I4 – I6 = 0

I2 – I1 – I3 = 0

По 2-му закону Кирхгофа составляем 6 – 3 = 3 ур-я.

- E1 = I1 * r1 + I4 * r4 – I3 * r3

O = I5 * r5 – I6 * r6 – I4 * r4

E2 = I2 * r2 + I3 * r3 + I6 * r6

используем метод контурных токов. Полагаем, что контурные токи текут в в контурах I, II и III по часовой стрелке. Поэтому получим:

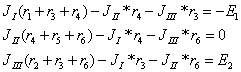
Подставляя числовые значения, получим систему:

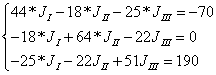
Решаем данную систему по формулам Крамера:

Т.о.

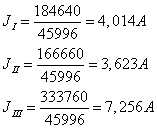
Следовательно, токи в ветвях равны:

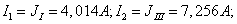
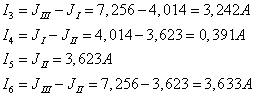
2)  определим режим работы активных ветвей

для источника Е1 направления движения ЭДС и тока I1 не совпадают, поэтому ветвь работает в режиме потребителя; для Е2 – направлены одинаково ветвь работает в режиме генератора.

Баланс мощности:

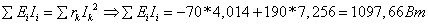
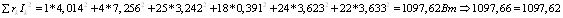
Задача 3. Расчет разветвленной цепи синусоидального переменного тока

Условие задачи. В цепи переменного тока, заданы параметры включенных в нее элементов, действующее значение и начальная фаза ψ U напряжения, а также частота питающего напряжения f = 50 Гц .

f = 50 Гц; U = 380B; ψ U = 150; r1 = 8Ом; L1 = 26мГн; C1 = 200миФ; r2 = 12Ом; r3 = 5Ом; L2 = 31мГн; L3 = 12мГн; C2 = 200миФ; C3 = 250миФ.

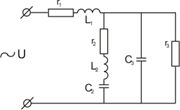
Решение

1)  Запишем сопротивления ветвей в комплексной форме.

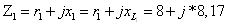
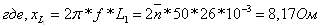
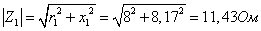
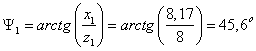
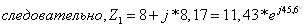
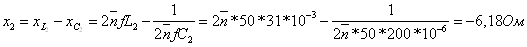
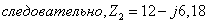
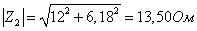
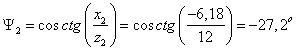
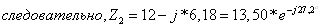
Объединяя С3 и r3 в одну ветвь, имеем:

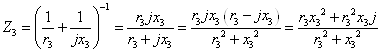
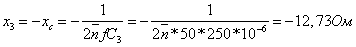
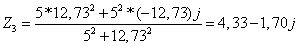
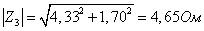
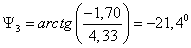
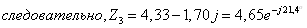
Найдем комплексное значение полного сопротивления на участие с параллельным соединением

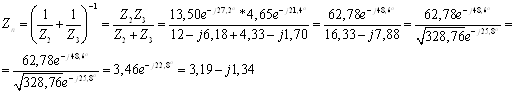
Общее сопротивление всей цепи:

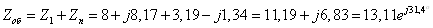
2)  напряжение источника в комплексной форме:

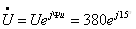
Тогда ток в неразветвленной части цепи:

Напряжение на участие с параллельным соединением ветвей:

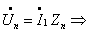
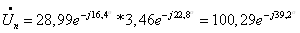
Токи в параллельных ветвях цепи:

Для ветви с r2, L2 и С2 имеем:

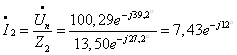
Для ветви с параллельным соединением r3 и С3:

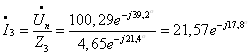
Для отдельно рассматриваемых r3 и С3 получим:

3)  мгновенные значения напряжения на участие цепи с параллельными соединением:

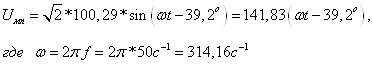
Для токов в ветвях имеем:

Неразветвленная часть цепи:

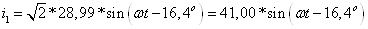
Для ветви с r2, L2 и С2:

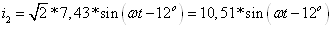
Для ветвей с параллельным соединением r3 и С3:

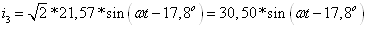
Для отдельно рассматриваемых r3 и С3:

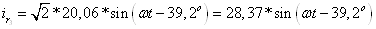
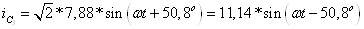
4)  строим векторную диаграмму по расчетным значениям токов и напряжений при этом учитываем, что

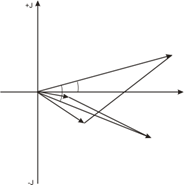
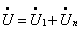
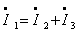
5)  полная мощность источника:

 ;

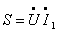где 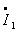 - сопряженное комплексное значение тока.

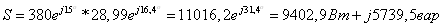
Активная мощность равна действительной части комплексного значения полной мощности: Р = 9402,9 Вт ; а реактивная – мнимой части : Q = =5739,5вар.

6)  баланс мощности

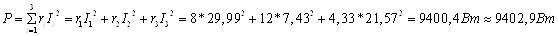
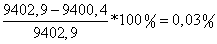 , Различие вызвано ошибками округления

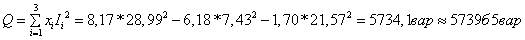
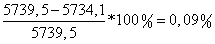 , вызвано ошибками округления

Итог: задача решена верно.

Задача 4. Расчет трехфазной цепи переменного тока

Условие задачи. К трехфазному источнику с симметричной системой фазных напряжений подключены сопротивления, распределение которых по фазам. Значения линейного напряжения Uл, активных r, индуктивных ХL и емкостных XC сопротивлений приемников. При расчете цепи пренебрегаем сопротивлением линейных и нейтрального проводов.

Требуется: 1) нарисовать схему соединения приемников в звезду с нулевым проводом; 2) определить токи в линейных и нейтральном проводах; 3) определить активную и реактивную мощности, потребляемые цепью; 4) построить векторную диаграмму; 5) включить эти же элементы приемника по схеме треугольника, определить фазные и линейные токи.

Вариант 1

Uл = 380В

Фаза А: r 1 = 6 Ом

Фаза В: r 2 = 6 Ом ; xL2 = 6 Ом

Фаза С: r 3 = 3 Ом ; xС3 = 5 Ом

Решение:

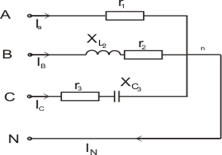
1)  Схема соединения в звезду с нулевым приводом:

2)  напряжения в фазах приемника в комплексной форме:

; ; ;

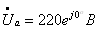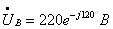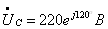где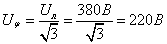

Модули и фазы сопротивлений:

;  

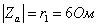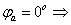
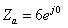
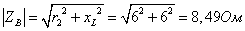
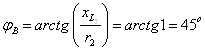
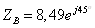
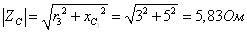
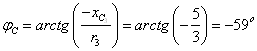
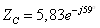
При соединении приемников в звезду токи линейные равны токам фазным, и определяются по закону Ома:

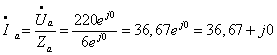
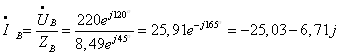
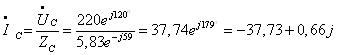
Ток в нейтральном проводе определяется по первому закону Кирхгофа:

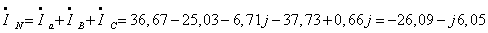
3)  определяем активную и реактивную мощности, потребляемые системой.

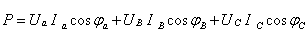
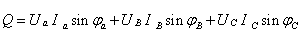
Где Ui и Ii –действующие значения токов и напряжений; ψi – сдвиг фаз между U и I.

Т.к. 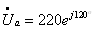;  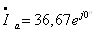, то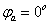

;  

 ;  

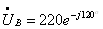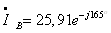
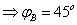
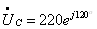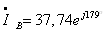
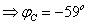
Следовательно,

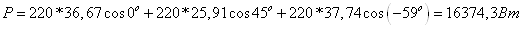
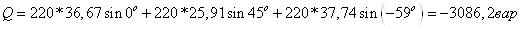
Полная мощность:

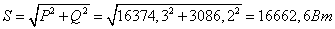
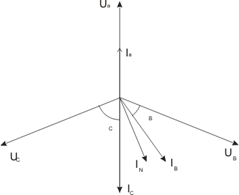
4)  векторную диаграмму строим по найденным значениям токов и напряжений.

Ток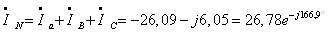

5)  при соединении нагрузки в треугольник для фазных напряжений имеем:

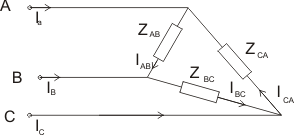
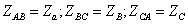
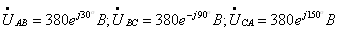
Токи в фазах приемника по закону Ома:

Токи в линейных проводах равны:

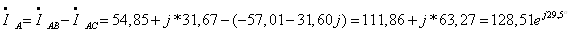
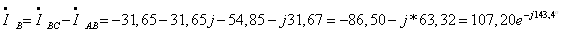
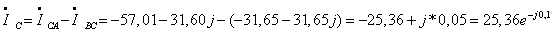
Из сравнения линейных токов для соединения в звезду и треугольник видно, что при соединении токи в в линейных проводах увеличиваются.