Курсовая работа: Методы и средства измерений
Аннотация
Данная расчетная работа выполнена на 35 листах печатного текста формата
А4, содержит 13 таблиц, 10 рисунков, 2 графика. В расчетной работе рассмотрены
следующие темы:
– методы и средства измерения температуры;
– методы и средства измерения давления;
– методы и средства измерения расхода;
– методы и средства измерения влажности и состав вещества.
Содержание
Введение
Задание 1.
Методы и средства измерений температуры
Задание 2.
Методы и средства измерений давления
Задание 3.
Методы и средства измерений расхода
Задание 4.
Приборы для измерения состава, влажности и свойств вещества
Заключение
Библиографический
список
Введение
В различные исторические периоды состояние мер и измерительной техники
находилось в прямой зависимости от хозяйственной деятельности, религиозных и
других факторов жизни общества.
В 1790 году Учредительным собранием Франции был поставлен вопрос о
создании и узаконении единой и обязательной для всех контролируемой государственной
системы мер. В 1799 году на хранение в архив Французской республики были
переданы платиновые эталоны метра и килограмма. Вся совокупность метрических
мер, созданных и узаконенных во Франции в конце XVIII века, легла в основу
метрической системы мер, некоторые единицы вошли в качестве основных в
Международную систему единиц (СИ).
Механика была первой из наук, где применялись единицы измерения. В
прошлом существовало несколько вариантов систем единиц, но постепенно
общепринятой стала система СГС (сантиметр, грамм, секунда). Затем была разработана
система МКС (метр, килограмм, секунда).
В 1867 году в Париже был организован Международный комитет мер и весов,
основная задача которого состояла в тщательном изучении метрических мер,
сравнение их с другими мерами, выявлении и разработке возможностей
использования их внутри каждой страны и для международных отношений.
Электроизмерительные приборы, имеющие более 250-летнюю историю, обязаны
своим развитием работам А. Вольта, А. Ампера, М. Фарадея. Им принадлежит
первенство в создании приборов прямого преобразования - гальванометров,
амперметров, вольтметров и т.д.
История создания приборов уравновешивающего преобразования начинается с
1841 года, когда были предложены мостовой метод измерения (мост Уитстона) и
компенсационный метод измерения постоянного напряжения (компенсатор
Поггендорфа). Кроме того, в XIX веке найдены основные принципы неэлектрических
величин в электрические: термоэлектрический эффект (Т. Зеетек, У. Томсон),
пьезоэффект, тензоэффект (О. Д. Хвольсон).
Дальнейшему развитию электроизмерительных приборов способствовало
изобретение электронной лампы: в 1904 году появился диод, а в 1910 году – триод
и пентод. Сочетание усилителей и выпрямителей с магнитоэлектрическим
измерительным механизмом позволило создать электронные вольтметры, частотомеры,
фазометры. Изобретение электронно-лучевой трубки в 1911 году привело к созданию
электронно-лучевого осциллографа, который стал универсальным электроизмерительным
прибором. Развитие электроники привело к разработке автоматических
компенсаторов и мостов. Таким образом, классическая электроизмерительная
техника дополнилась приборами с автоматическим уравновешиванием и электронными
измерительными приборами.
ЗАДАНИЕ 1. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ ТЕМПЕРАТУРЫ
1.1 Термопара, имеющая сопротивление Rвн,
подключена к милливольтметру с внутренним сопротивлением Rv,
измерения проводятся в диапазоне ДИ.
Требуется:
1.
Изобразить схему подключения термопары к милливольтметру.
2.
Определить диапазон изменения напряжения на выводах милливольтметра при
температуре свободных концов термопары, если Т0 = 0 °С.
3.
Определить систематическую погрешность, если Т0 = 20 °С.
4.
Определить систематическую погрешность, если сопротивление подключаемых
проводов будет по 5 Ом.
Решение
Исходные данные сводим в табл. 1.1.
Таблица 1.1
Исходные данные
| Параметр |
Обозначение |
Значение |
|
1. Внутреннее
сопротивление вольтметра
|
Rвн
|
14 Ом |
|
2. Сопротивление
измерительной цепи
|
Rv
|
190 Ом |
| 3. Диапазон измерений |
ДИ |
0…160°С |
| 4. Тип термопары |
ТХК(L) |
- |
1.1.1 Схема подключения термопары к милливольтметру
Схема подключения термопары к милливольтметру приведена на рис. 1.1.
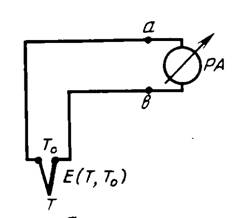
Рис. 1.1. Схема измерения ТЭДС милливольтметром
1.1.2 Определяем диапазон изменения напряжения на выводах милливольтметра
Определяем диапазон изменения напряжения на выводах милливольтметра при
температуре свободных концов термопары, если Т0 = 0 °С, по формуле:
Uав = Е(T, T0)/(1+Rвн/Rv), (1.1)
где Е(T, T0) –
ТЭДС термопары, мВ, при температуре Т горячих спаев (измерительных спаев) и Т0
– холодных спаев, °С; Rv – внутреннее
сопротивление вольтметра, Ом; Rвн – сопротивление
измерительной цепи, в которое входит сопротивление термопары, соединительных
проводов, контактов и т.п., Ом.
По таблице П12 приложения определяем значения ТЭДС термопары ТХК(L) при 0 °С и при + 160 °С.
Е ( 0) = 0,000 мВ.
Е (+ 160, 0) = + 11,398 мВ.
Полученные значения подставляем в формулу (1.1)
Uав(0°С) = 0,000 /(1+14/190) = 0,000 мВ
Uав(+160°С) = +11,398 /(1+14/190) = 10,615
мВ.
1.1.3 Определяем диапазон изменения напряжения на выводах милливольтметра
и систематическую погрешность, если Т0 = 20 °С
По таблице П9 приложения определяем значения ТЭДС термопары ТХК(L) при 0 °С и при + 160 °С , если Т0 = 20 °С
Е (0, 20) = 0,000 – 1,290 = – 3,133 мВ.
Е (+ 160, 20) = + 11,398 – 1,290 = 10,108 мВ.
Полученные значения подставляем в формулу (1.1)
Uав(0°С; +20 °С) = – 1,290/(1+14/190)
= – 2,947 мВ
Uав(+160°С; +20 °С) = + 10,108/(1+14/190)
= + 10,108 мВ.
DUав
= Uав(–30°С; +20 °С) – Uав(–30°С)
= – 1,290 – 0,000 = – 1,290 мВ.
Таким образом, в показании милливольтметра будет присутствовать аддитивная
систематическая погрешность DUав = –1,290 мВ, которую необходимо учитывать при
измерениях. В виде приведенной погрешности это значение составит
g = DUав/XN × 100 %,
где XN –
нормализующее значение изменяемой величины.
g= 1,290/(+ 10,615 – 0,000) × 100 % = 12,1 %,
что достаточно велико.
1.1.4 Определяем систематическую погрешность, если сопротивление подключаемых
проводов будет по 5 Ом
При наличии двух соединительных проводов с сопротивлением по 5 Ом каждый
сопротивление измерительной цепи увеличится на 10 Ом и составит
R¢вн
= 14 + 10 = 24 Ом.
Полученное значение подставляем в формулу (1.1)
U¢ав(–30°С)
= 0,000/(1+24/190) = 0,000 мВ
U¢ав(+180°С)
= + 11,398/(1+24/190) = 10,119 мВ.
DU¢ав = U¢ав(0°С)
– Uав(0°С) = 0,000 мВ.
DU¢ав = U¢ав(+160°С)
– Uав(+160°С) = + 10,119 – 10,615 = – 0,496
мВ.
Таким образом, в показании милливольтметра будет присутствовать мультипликативная
систематическая погрешность, изменяющаяся в зависимости от показаний прибора
следующим образом (табл. 12.4), которую необходимо учитывать при измерениях.
В виде приведенной погрешности это значение составит
g = –0%,
g = 0,496/(+10,615 - 0) ×100 = 4,67%,
что достаточно велико.
Таблица 1.2
Динамика мультипликативной систематической погрешности от наличия неучтенного
сопротивления проводов
|
Измеряемое значение
температуры
|
Показания прибора, мВ |
Значение
погрешности, мВ
|
| истинное |
реальное |
| 0 |
0 |
0 |
0 |
| 40 |
2,443 |
2,329 |
0,114 |
| 80 |
5,042 |
4,805 |
0,237 |
| 120 |
7,771 |
7,408 |
0,363 |
| 160 °С |
10,615 |
10,119 |
0,496 |
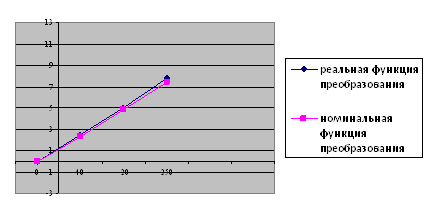
1.2 Измерение температуры с помощью термопары подключенной к потенциометру
Рассмотрим методику решения задач на примере. ТЭДС измеряется с помощью
потенциометра, в котором используется нормальный элемент с ЭДС Енэ =
1,01183 В, который имеет сопротивление Rнэ.
Требуется:
1. Изобразить
принципиальную схему потенциометра.
2. Определить
значения ТЭДС для заданной термопары, если уравновешивание произошло при
сопротивлениях Rр1 и Rр2.
3. Определить
погрешность потенциометра при падении ЭДС нормального элемента на величину DЕнэ
Решение
Исходные данные сводим в табл. 1.2.
Таблица 1.2
Исходные данные
| Параметр |
Обозначение |
Значение |
| 1. ЭДС нормального элемента |
Енэ
|
1,01183 В |
| 2. Падение ЭДС |
DЕнэ
|
1,33 мВ |
| 3. Сопротивление нормального элемента |
Rнэ
|
190 кОм |
| 4. Сопротивления, при которых произошло уравновешивание |
Rр1
Rр2
|
0,42 Ом
0,21 Ом
|
| 5. Тип термопары |
ТПП(R) |
- |
1.2.1 Схема подключения термопары к потенциометру
Схема подключения термопары к потенциометру приведена на рис. 1.2.
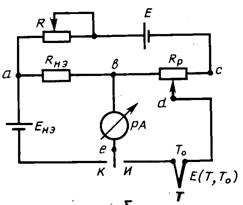
Рис. 1.2. Схема измерения ТЭДС потенциометром
1.2.2 Определяем значения ТЭДС для заданной термопары
Значения ТЭДС, если уравновешивание произошло при сопротивлениях Rр1 и Rр2,
определяем по формуле:
Е(T, T0) = I×Rbd = Eнэ×Rbd/Rнэ, (1.2)
где I = Eнэ/Rнэ – ток в измерительной цепи ас, А;
Eнэ – ЭДС нормального (образцового)
элемента питания, В;
Rнэ – сопротивление нормального
элемента питания, Ом;
Rbd – часть сопротивления Rр, при котором произошло уравновешивание, Ом.
Е(T, T0)1
= 1,01183 ×0,42/190 =
0,0022367 В = 2,237 мВ.
Е(T, T0)2
= 1,01183 ×0,21/190 = 0,0011183
В = 1,118 мВ.
Для термопары ТХK(L) по
таблице П8 приложения определяем значения температуры
Е(+ 283) = 2,236 мВ.
Е(+ 160) = 1,118 мВ.
1.2.3 Определяем погрешность потенциометра при падении ЭДС нормального элемента
Определяем ТЭДС при падении ЭДС нормального элемента на величину DЕнэ = 1,33 мВ по формуле (1.2)
Е¢(T,
T0)1 = (1,01183 – 0,00133) ×0,42/190 = 0,00223 В = 2,238
мВ.
Е¢(T,
T0)2 = (1,01183 – 0,00133) ×0,21/190 = 0,0011624 В = 1,162
мВ.
Определяем погрешность измерения ТЭДС
DЕ(T, T0)1= Е¢(T, T0)1 – Е(T, T0)1 = 2,238
– 2,237 = 0,001 мВ.
DЕ(T, T0)2= Е¢(T, T0)2 – Е(T, T0)2 = 1,162
– 1,118 = 0,044 мВ.
Погрешность является систематической мультипликативной, в относительном
виде она равна:
δ1 = DЕ(T, T0)1/Е(T, T0)1×100 % = 0,001/2,237×100 % = 0,04 %.
δ2 = DЕ(T, T0)2/Е(T, T0)1×100 % = 0,044/1,118 ×100 % = 3,94%.
1.3 Измерение температуры с помощью термосопротивления, включенного в
уравновешенный мост
При измерении термосопротивления с помощью уравновешенного моста известны
сопротивления плеч R1 и R2,
тип термосопротивления и диапазон измерения.
Требуется:
1. Изобразить
принципиальную схему уравновешенного моста.
2. Определить
полное сопротивление переменного резистора R3
и цену деления шкалы (°С/Ом).
3. Оценить
погрешность измерения температуры в верхнем пределе измерений для заданного
класса допуска ТС.
4. Определить
погрешность прибора, если резисторы R1 и R2 имеют допуски ± 0,5 %.
5. Определить
погрешность измерения при наличии сопротивления проводов 0,5 Ом.
Решение
Исходные данные сводим в табл. 1.4.
Таблица 1.4
Исходные данные
| Параметр |
Обозначение |
Значение |
| Диапазон измерений |
ДИ |
-50…+150 °С |
| Сопротивления |
R1
R2
|
1,3 кОм
6 кОм
|
| Тип термосопротивления |
ТСМ 50 |
50
м при 0°С |
| Класс допуска |
- |
С |
1.3.1 Схема подключения термосопротивления к уравновешенному мосту
Схема подключения термосопротивления к уравновешенному мосту приведена на
рис. 1.3.
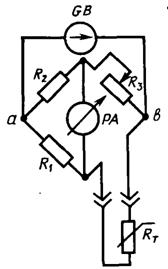
Рис. 1.3. Схема измерения термосопротивления с помощью уравновешенного моста
1.3.2 Определение полного сопротивления переменного резистора R3 и цену деления шкалы (°С/Ом)
Полное сопротивление переменного резистора R3
определяем по закону Кирхгофа:
R1R3=R2R4, (1.3)
откуда
R3=R2R4/ R1, (1.4)
При 0 °С получим
R3-0°С =6000·50/ 1300=230,8 Ом.
Значения сопротивления от температуры определяем по формулам:
платиновые в диапазоне от 0 до 600 °С
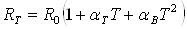 (1.5)
(1.5)
в диапазоне от – 200 до 0 °С
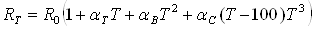 (1.6)
(1.6)
где αT =
3,9692 × 10-3
1/°К, αВ = 5,8290 ×
10-7 1/°К2 и αС = 4,3303 × 10-12 1/°К3
– температурные коэффициенты сопротивления.
Медные в диапазоне от – 50 до + 150 °С
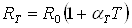 , (1.7)
, (1.7)
в диапазоне от – 100 до – 10 °С
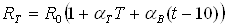 , (1.8)
, (1.8)
где αT =
4,28 × 10-3
1/°К и αВ = 5,4136 ×
10-7 1/°К2.
При -50°С получим
RТ-50=50·(1+3,9692·10-3(-50)+5,8290·10-7·(-50)2+4,3303·10-12(-50-100)·(-50)3)
=78,46 Ом.
R3-50°С=6000·78,46 /1300=362,215 Ом
При +150°С получим
RТ+150=50·(1+3,9692·10-3(+150)+5,8290·10-7·(+150)2)
=164,20 Ом.
R3+100°С=6000·164,20/1300=757,846 Ом
Диапазон изменения сопротивлений переменного резистора
R3=362,215…757,846 Ом при изменении
температуры от -50 до +150 °С.
Цена деления шкалы составит
ЦД=(150-(-50))/( 757,846-362,215)=0,5 °С/Ом.
1.3.3 Определяем погрешность измерения температуры в верхнем пределе
измерений, для заданного класса допуска ТС
В нашем случае используется ТСМ 50 класса допуска В. Допускаемые отклонения
сопротивлений от номинального значения ТСП при 0 °С для класса В:±0,05%.
RТ150,2=164,415 Ом,
RТ149,2=163,985 Ом.
Размах показаний прибора в верхнем пределе диапазона измерений (+200
оС) составит RТ150,2- RТ149,2=164,415-163,985=0,43 Ом. Таким образом, абсолютная
погрешность измерения температуры составит ΔТ=±0,4 оС
Погрешность будет иметь как аддитивный, так и мультипликативный характер.
1.3.4 Определяем погрешность прибора, если резисторы R1
и R2 имеют допуски ± 0,5 %
Из анализа формулы (1.3) видно, что
R4 = R1×R3
/R2. (1.9)
Поэтому, при Т = 0 °С:
R4max = R1max×R3/R2min,
R4min = R1min×R3/R2max,
R4max = 6000×(1,005)× 230,8/(1300×0,995) = 10,7593 = 10,76 Ом,
R4min = 6000×(0,995)× 230,8/(1300×1,005) = 10,5463 = 10,54 Ом.
По формуле приведения
Т = Т1 + (Т2 – Т1)×(R – R1)/(R2 – R1), (1.10)
где R2 и R1
– наибольшее и наименьшее значения интервала сопротивлений, в который входит
известное значение R; Т1 и Т2 –
наименьшее и наибольшее значения интервала температуры в который входит искомое
значение Т.
В градуировочной таблице рассчитанные по формуле (1.9) от +2 +3 °С и от
-2– 3 °С), поэтому
Т = 2 + (3 – 2)×(50,50 – 50,39)/(50,585
– 50,39) = +2,564 °С.
Т = -2 + (–3 –(-2))×(49,50
– 49,661)/(49,4165 – 49,661) = – 2,571 °С.
Таким образом, погрешность измерений составит DТ = ± 2,5 °С.
1.3.5 Определяем погрешность измерения при наличии сопротивления проводов
0,5 Ом
Соединительные провода (2 шт.) подключены к термосопротивлению, поэтому
при Т = 0 °С истинное сопротивление будет равно
R4 = R1×R3
/R2 – 2RП = 50 – 0,5 – 0,5 =
49 Ом.
Поэтому систематическая аддитивная погрешность составит
DТ = -5 + (-6-(-5))×(49,00 – 49,0225)/(47,328 – 49,0225) =
– 5,013 °С.
1.4 Измерение температуры с помощью термосопротивления, включенного в
неуравновешенный мост
неуравновешенный мост включено термосопротивление, шкала миллиамперметра
имеет заданный диапазон измерений, напряжение питания моста Uab,
известны также сопротивления плеч моста R2 и
R3.
Требуется:
1. Изобразить
принципиальную схему неуравновешенного моста.
2. Определить
сопротивление R1, если Т0 = 0 °С.
3. Построить
график I = f(T),
в пределах диапазона измерений и определить цену деления шкалы (мА/°С).
4. Определить
погрешность измерения, связанную с нелинейностью функции преобразования.
5. Определить
погрешность измерений при наличии допуска на номинальное сопротивление
терморезистора ± 0,1 Ом.
6. Определить
погрешность измерений при падении напряжения на 0,2 В.
Решение
Исходные данные сводим в табл. 1.5.
Таблица 1.5
Исходные данные
| Параметр |
Обозначение |
Значение |
| 1. Диапазон измерений |
ДИ |
± 60
°С |
| 2. Сопротивления |
R2
R3
|
280 Ом
35 Ом
|
| 3. Тип термосопротивления |
ТСП 100 |
100 Ом при 0°С |
| 4. Напряжение питания |
Uab
|
5 В |
1.4.1 Схема подключения термосопротивления к неуравновешенному мосту
Схема подключения термосопротивления к неуравновешенному мосту приведена
на рис. 1.4.
1.4.2 Определяем сопротивление R1 при
условии Т0 = 0 °С
Сопротивление резистора R1 определяем
по закону Кирхгофа (1.5)
R1 = R2×R4
/R3, (1.9)
R1 = 280×100/35 = 800 Ом.
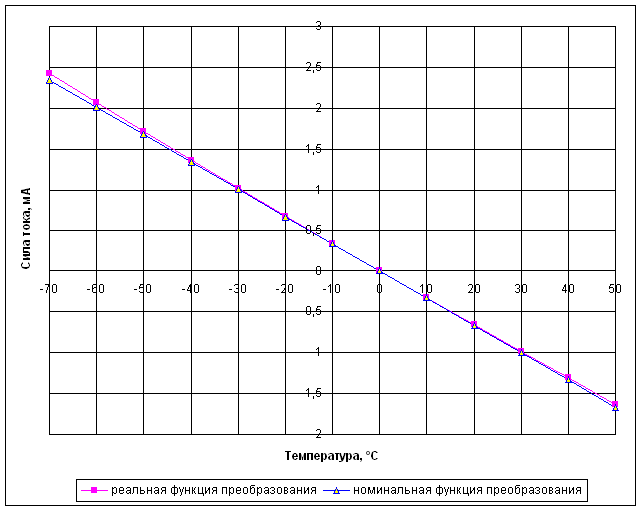
1.4.3 Строим график I = f(T) в пределах диапазона измерений и определяем цену деления
шкалы (мА/°С)
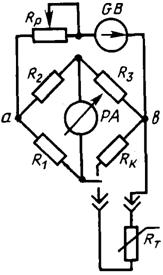
Рис. 1.4. Схема измерения термосопротивления с помощью неуравновешенного
моста
Зависимость силы тока от изменения сопротивления для неуравновешенного
моста определяется по формуле
 , (1.10)
, (1.10)

после преобразований получим:
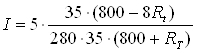
Для удобства перейдем в миллиамперы:
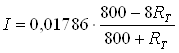 (1.11)
(1.11)
На основании зависимости (1.11) можно построить таблицу и график изменения
силы тока в диагонали измерительного моста в зависимости от изменения
сопротивления термопреобразователя и температуры в пределах заданного диапазона
измерений.
Таблица 1.5
Зависимость силы тока от величины термосопротивления и температуры
| Температура Т, °С |
Сопротивление термопреобразователя RT, Ом
|
Сила тока I,
мА |
Значения линейной функции Iл, мА
|
Цена деления, мА/°С |
| – 70 |
7,233 |
2,430 |
2,345 |
- 0,0347143 |
| – 60 |
7,633 |
2,076 |
2,010 |
- 0,0346 |
| – 50 |
8,031 |
1,719 |
1,675 |
- 0,03438 |
| – 40 |
8,427 |
1,367 |
1,340 |
- 0,034175 |
| – 30 |
8,822 |
1,019 |
1,005 |
- 0,0339667 |
| – 20 |
9,216 |
0,675 |
0,670 |
- 0,03375 |
| – 10 |
9,609 |
0,335 |
0,335 |
- 0,0335 |
| 0 |
10,00 |
0 |
0 |
- |
| 10 |
10,39 |
- 0,331 |
- 0,331 |
- 0,0331 |
| 20 |
10,779 |
-0,659 |
- 0,662 |
- 0,03295 |
| 30 |
11,167 |
- 0,984 |
- 0,997 |
- 0,0328 |
| 40 |
11,554 |
- 1,304 |
- 1,332 |
- 0,0326 |
| 50 |
11,940 |
- 1,246 |
-1,667 |
- 0,02492 |
| 60 |
12,324 |
- 1,935 |
- 2,002 |
- 0,03225 |
| 70 |
12,708 |
- 2,245 |
- 2,337 |
- 0,0320714 |
|
|
|
|
|
|
1.4.4 Определяем погрешность измерения, связанную с нелинейностью функции
преобразования
Наибольшая величина погрешности от нелинейности функции преобразования в
пределах диапазона измерений составит
Dл = I – Iл = -2,245- (- 2,337)
= - 0,092мА.
В относительном виде
dл = Dл/Imax ×100
% = - 0,092/ 2,430*100= - 3,79 %.
1.4.5 Определяем погрешность измерений при наличии допуска на номинальное
сопротивление терморезистора ± 0,1 Ом
Подставим в формулу (1.11) значения 10 ±
0,1 Ом, получим:
Погрешность измерений при наличии допуска на номинальное сопротивление
терморезистора ± 0,1 Ом составит DR =± 0,085 мА.
В приведенном виде
g = DR/(Imax
– Imin)×100 % = ± 0,085/
(2,430 – ( - 2,245)) 100 % = ± 1,81 %.
1.4.6 Определить погрешность измерений при падении напряжения
Подставим в формулу (1.11) значение напряжения Uав
= 5 – 0,2 = 4,8 В.
Наибольшая величина погрешности от падения напряжения питания составит
Du = I¢max – Imax = – 2,1 –
(–2,245) = 0,145 мА.
В относительном виде
du
= Du/Imax ×100 % = 0,145/(– 2,245) ×100 % = - 6,45 %.
Выводы:
1. Шкала измерительного прибора, отградуированная в градусах Цельсия,
будет иметь погрешность нелинейности, увеличивающуюся к концу диапазона
измерений и равную dл = – 3,79
%, это связано с тем, что величина R4 = RT входит в числитель и знаменатель выражения
(1.10), являющимся теоретическим выражением функции преобразования для
неуравновешенного моста.
2. Погрешность измерений при наличии допуска на номинальное сопротивление
терморезистора ± 0,1 Ом в приведенном
виде равна g = ± 1,81 %, она будет оказывать незначительное влияние на
погрешность измерений.
3. Погрешность измерений из-за падения напряжения питания на 0,2 В в
относительном виде равна du = – 6,45 %, поэтому падение напряжения при применении
неуравновешенного моста будет оказывать существенное влияние на результат
измерений.
ЗАДАНИЕ 2. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ ДАВЛЕНИЯ
2.1 Пружинная мембрана манометра диаметром D,
толщиной h и модулем упругости ЕG деформируется под действием давления от 0 до
δmах.
Требуется:
1. Изобразить схему мембраны деформационного манометра.
2. Определить диапазон измеряемых давлений.
3. Определить погрешность измерений, если толщина пружины h выполнена с допуском ±0,01 мм.
4.
Сделать заключение о соответствии манометра заданному классу точности.
Решение
Исходные данные сводим в табл. 2.1.
Таблица 2.1
Исходные данные
| Параметр |
Обозначение |
Значение |
| 1. Толщина, мм |
h |
0,8 мм |
| 2. Диаметр, мм |
D |
86 мм |
| 3.Модуль упругости |
ЕG
|
92 ГПа |
| 4.Допустимое напряжение мембраны |
σmах
|
600 МПа |
| 5. Начальное напряжение мембраны |
σ0
|
55 МПа |
| 6. Класс точности |
- |
1.6 |
| 7.Перемещение центра мембраны, мм |
δ1
|
0,45 |
2.1.1 Схема мембраны деформационного манометра
Схема мембраны деформационного манометра приведена на рис. 2.1.
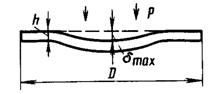
Рис. 2.1. Схема мембраны деформационного манометра
2.1.2 Определяем диапазон измеряемых давлений
Механическое напряжение на мембране определяется по формуле
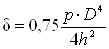 , (2.1)
, (2.1)
где p – давление, Па; D –
диаметр мембраны, мм; h – толщина мембраны, мм.
Из формулы (2.1) определяем диапазон измерения давлений при заданных
значениях напряжения мембраны:
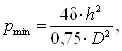
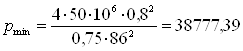 Па
Па
Верхний предел измерения
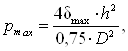
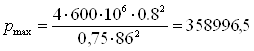 Па
Па
2.1.3 Определение результата измерения давления при перемещении центра
мембраны δ1
Деформация мембраны связана с давлением следующим соотношением
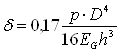 , (2.2)
, (2.2)
выразим отсюда давление
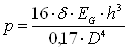 , (2.3)
, (2.3)
Таким образом, при перемещении мембраны δ1=0,35 мм
давление составит
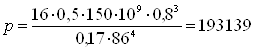 Па
Па
2.1.4 Определение погрешности результата измерения по классу точности
манометра
При заданном классе точности 1,0 нормируемое значение абсолютной погрешности
измерений будет равно
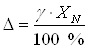 ,
,
Где γ – приведенная погрешность манометра, % ; 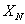 - нормирующее значение, Па:
в нашем случае, т.к. рmax = 358996.5 Па принимаем, что
верхний предел измерения манометра 350 кПа,т.е.
- нормирующее значение, Па:
в нашем случае, т.к. рmax = 358996.5 Па принимаем, что
верхний предел измерения манометра 350 кПа,т.е. 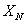 =
350000 Па.
=
350000 Па.
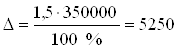 Па
Па
Запишем результат измерений
Р=(193139±5250) Па
2.1.5 Определяем погрешность измерений, если толщина пружины h выполнена с допуском ±0,01 мм
Подставим в зависимость (2.1) значения наибольшего давления и величину h с наибольшим и наименьшим размерам
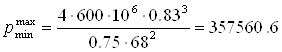 Па
Па
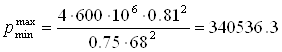 Па
Па
Наибольшую абсолютную погрешность определяем по выражению
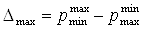
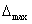 = 357560.6-340536.3=17024,3
Па
= 357560.6-340536.3=17024,3
Па
Подставим в зависимость (2,1) значения минимального давления и величину h с набольшими и наименьшими размерами
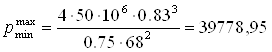 Па
Па
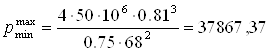 Па
Па
Минимальную абсолютную погрешность определяем по выражению
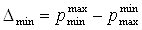
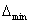 =39778,95-37837,37=1941,58
Па
=39778,95-37837,37=1941,58
Па
Таким образом, видно, что погрешность от допуска на изготовления толщины
мембраны зависит от измеряемого давления, т.е. является мультипликативной
2.2 Измерение давления трубчато – пружинным деформационным манометром
В трубчато-пружинном манометре однотрубная пружина радиусом R0 с первоначальным углом закручивания α =
270° и параметрами поперечного сечения а и b, выполнена
из материала с модулем упругости ЕG.
Требуется:
1. Изобразить схему пружинно-трубчатого манометра
2. Определить изменения угла закручивания и угла перемещения конца
пружины при заданном наибольшем давлении рmах.
3. Определить погрешность измерений, если диаметр трубки D0 выполнен с допуском ±1,0 мм.
4. Назначить класс точности манометра, с учетом запаса точности 2,5.
Решение
Исходные данные сводим в табл. 2.2.
Таблица 2.2
Исходные данные
| Параметр |
Обозначение |
Значение |
| 1. Радиус |
R0
|
32 мм |
| 2. Параметры поперечного сечения |
а
b
|
19мм
7,2 мм
|
| 3.Контролируемый параметр |
р |
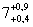 МПа МПа
|
| 4. Модуль упругости материала |
ЕG
|
195 ГПа |
2.2.1 Схема пружинно-трубчатого манометра
Схема пружинно-трубчатого манометра приведена на рис. 2.2.
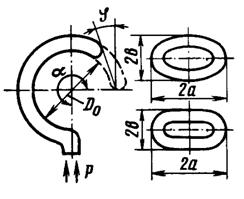
Рис. 2.2. Схема пружинно-трубчатого манометра
2.2.2 Выбор класса точности трубчато-пружинного манометра для контроля
параметра p
Определяем допуск контролируемого параметра
T=pmax - pmin (2.1)
где pmax – наибольшее значение
контролируемого параметра, Па; pmin - минимальное
значение контролируемого параметра, МПа.
Для контролируемого параметра 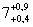 МПа;
МПа;
наибольшее давление pmax=7,9 МПа;
минимальное давление pmin=7,4 МПа
T=7,9-7,4=0,5 МПа
Допускаемая погрешность измерения контролируемого параметра определяем по
формуле:
δизм=0,33 T (2.2)
δизм=0,33·0,5=0,165 МПа
Пределы измерения манометра определяем по формулам:
Нижний предел измерения
HДИ ≤ pmin
- δизм; (2.3)
HДИ ≤ 7,4 – 0,165 =7,235 МПа;
верхний предел измерения
ВДИ ≤ pmax +δизм; (2.4)
ВДИ ≤7,9+0,165=8,065 МПа
В соответствии с определенными значениями HДИ
и ВДИ выбираем манометр с верхним пределом измерений 10 МПа.
Приведенную погрешность манометра определяем по формуле
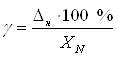 (2.5)
(2.5)
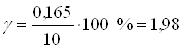 Па
Па
По найденному значению основной приведенной погрешности выбираем манометр
класса точности 1,6.
2.2.3 Определяем изменение угла закручивания и угла перемещения конца
пружины при заданном наибольшем давлении
Угла закручивания связано с давлением соотношением
 , (2.6)
, (2.6)
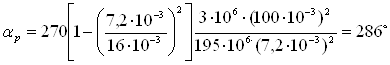
Изменение угла закручивания определяем по формуле
Δα=αр – α0 (2.7)
Δα=286° - 270=16°.
2.2.3 Определяем погрешность измерения, если диаметр трубки D0 выполнен с допуском ±1,0 мм.
Из формулы (2.6) выразим давление
 (2.8)
(2.8)
Подставим в зависимость (2.6) величину D0
с наибольшим и наименьшим размерами
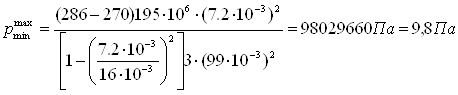
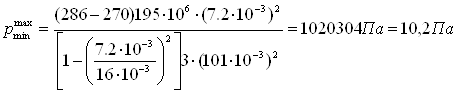
Максимальную абсолютную погрешность определим по выражению
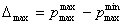 =1,99-1,91=0,08 МПа
=1,99-1,91=0,08 МПа
Погрешность является мультипликативной, т.к. зависит от измеряемого
параметра.
2.3 Измерение давления с помощью пьезоэлектрического преобразователя
Напряжение на пьезокристалле кварца преобразователя давления меняется от Umin до Umах,
причем используется n пластин толщиной h и размером a ´ b. Емкость измерительной цепи Свх = 10 пФ.
Пьезоэлектрическая постоянная для кварца k0
= 2,2×10-12 Кл/Н и
относительная диэлектрическая проницаемость e
= 4,5.
Требуется:
1. Изобразить схему пьезокристалла с заданным количеством пластин.
2. Определить диапазон измерения давления для заданных напряжений
3. Определить систематическую погрешность от влияния внешних физичских
величин, в результате чего емкость измерительной цепи Свх увеличится
на 5 %.
Решение
Исходные данные сводим в табл. 2.3.
Таблица 2.3
Исходные данные
| Параметр |
Обозначение |
Значение |
| 1. Число пластин n |
n |
4 |
| 2. Размеры пластины |
а
b
|
15 мм
15 мм
|
| 3. Толщина пластины |
h |
0,95 мм |
| 4. Наименьшее напряжение |
Umin
|
2 В |
| 5. Наибольшее напряжение |
Umах
|
46 В |
2.3.1 Схема пьезокристалла
Схема пьезокристалла приведена на рис. 2.3.
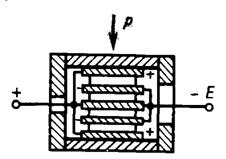
Рис. 2.3. Схема пьезокристалла
2.3.2 Определяем диапазон измерения давления для заданных напряжений
Значения давлений определяем по формуле:
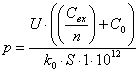 (2.5)
(2.5)
где S – площадь поверхности грани кристалла, м2;
Свх – емкость измерительной цепи, пФ; С0 – емкость
кристалла, пФ; n – число пластинок.
Емкость пьезокристалла определяем по соотношению
С0 = 8,9×e×S/h,
где h – толщина кристалла, м; e = 4,5 – относительная диэлектрическая проницаемость.
С0 = 8,9×4,5×(0,015·0,018)/0,6×10–3 = 0,01081×10–3 пФ.
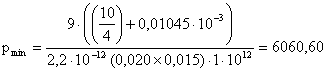 Па
Па
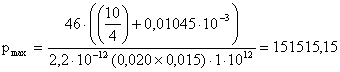 Па
Па
2.3.3 Определяем систематическую погрешность от влияния внешних физических
величин, в результате чего емкость измерительной цепи Свх увеличится
на 5 %
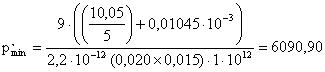 Па
Па
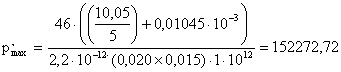 Па
Па
Dpmin
= p¢min – pmin=6090.90-6060.90=30.30
Па
Dpmax
= p¢max – pmax = 152272.72-151515.15=757.57
Па.
Таким образом, увеличение емкость измерительной цепи Свх на 5
% приведет к возникновению мультипликативной систематической погрешности.
ЗАДАНИЕ 3. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ РАСХОДА
3.1 Турбинный тахометрический расходомер с диаметром турбины d, постоянным коэффициентом эффективности k,
наружным диаметром трубопровода D, количеством лопастей
N, подключен к усилителю со встроенным вольтметром и
имеет частоту вращения турбины от 0 до nmax,
что соответствует изменению напряжения от 0 до Umax.
Требуется:
1. Изобразить схему турбинного тахометрического расходомера.
2. Определить шаг лопастей.
3. Определить диапазон измерения расхода жидкости.
4. Определить чувствительность прибора, В/(м3/ч).
5. Определить погрешность измерения расхода при допуске изготовления
наружного диаметра трубопровода D+ 0, 2 мм.
Решение
Исходные данные сводим в табл. 3.1.
Таблица 3.1
Исходные данные
| Параметр |
Обозначение |
Значение |
| 1. Диаметр турбины |
d |
60 мм |
| 2. Диапазон измерения частоты вращения турбины |
nmax
nmin
|
1800 мин -1
350 мин -1
|
| 3. Наименьшее измеряемое напряжение |
Umin
|
14 В |
| 4. Диаметр трубопровода |
D |
80 мм |
| 5. Коэффициент эффективности |
k |
0,70 |
| 6.Количество лопастей |
N |
8 |
| 7,Показания вольтметра |
U |
32 В |
| 8.Класс точности вольтметра |
- |
2 |
3.1.1 Схема турбинного тахометрического расходомера
Схема турбинного тахометрического расходомера приведена на рис. 3.1.
3.1.2. Определяем шаг лопастей
В турбинном расходомере расход жидкости определяют по формуле
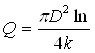 (3.1)
(3.1)
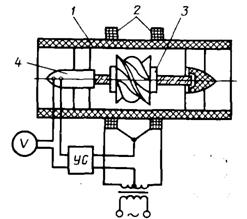
Рис. 3.1. Схема турбинного тахометрического расходомера
где l – шаг лопасти турбины, м.
Шаг лопастей определяем по формуле
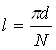 (3.2)
(3.2)
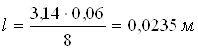
Нижний предел измерения расхода жидкости определяем по формуле
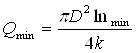 (3.3)
(3.3)
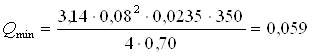 м3/мин
=3,54 м3/ч
м3/мин
=3,54 м3/ч
Нижний предел измерения расхода жидкости определяем по формуле
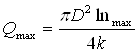 (3.4)
(3.4)
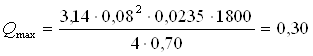 м3/мин
=18,2 м3/ч
м3/мин
=18,2 м3/ч
3.1.3 Определение частоты вращения и расхода по показанию вольтметра
Расход, соответствующий показанию вольтметра, можно определить по формуле
Q=CU (3.5)
где С – цена деления вольтметра, м3/(В·ч)
С=2,4/14=0,171 м3/(В·ч)
При показании вольтметра U=32 В расход следующий:
Q=0,171·32=5,472 м3/ч.
Частоту вращения, соответствующую показанию вольтметра, можно определить
по формуле
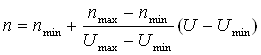 , (3.6)
, (3.6)
Где Umax –показание вольтметра,
соответствующее наибольшему расходу, В: при Qmax
=18,2 м3/ч из формулы (3,4) Umax = 160,8 В.
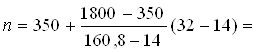 527,79 мин-1
527,79 мин-1
3.1.4 Определение абсолютной погрешности измерения расхода по классу
точности вольтметра
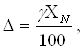 (3.7)
(3.7)
где γ – приведенная погрешность вольтметра, %; XN
- нормирующее значение, В: в нашем случае, т.к. Umax =160,8 В принимаем,что верхний предел измерения
вольтметра 170В, т.е. ХN =170 В
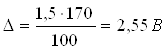
Абсолютная погрешность измерения расхода с учетом цены деления вольтметра
ΔQ=2,55·0,171=0,436 м3
3.1.5 Определяем погрешность измерения расхода при допуске изготовления
наружного диаметра трубопровода D+ 0, 2 мм.
Расход на верхнем пределе измерений с увеличенным диаметром определяем по
формуле
Q’min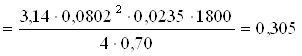 м3/мин =18,31 м3/ч
м3/мин =18,31 м3/ч
Погрешность измерений составит
D = Q¢max – Qmax
D =18.31-18,2=0.11 м3/ч
3.1.6 Определение суммарной погрешности измерения расхода
Суммарную погрешность измерения с учетом погрешности вольтметра и
изготовления наружного диаметра трубопровода определяем по формуле
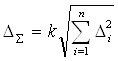 , (3.8)
, (3.8)
где k – поправочный коэффициент, зависящий от числа
слагаемых n, их соотношения и доверительной вероятности
при Pд: в нашем случае при n=2,
Pд=0,95 принимаем k=
1,1[5].
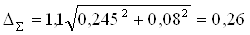 м3/ч
м3/ч
Тогда результат измерения при показаниях вольтметра U=32
В запишем так:
Q = (6,53±0,26)
3.2 Измерение расхода с помощью индукционного расходомера
Индукционный расходомер установлен на трубопроводе внутренним диаметром d, наружным диаметром D, при его
градуировке верхнему пределу измерений расхода Qmax
соответствует ЭДС Еmax.
Требуется:
1. Изобразить схему индукционного расходомера.
2. Определить расход при показании вольтметра U.
3. Определить абсолютную погрешность измерения расхода по классу точности
вольтметра.
4. Определить погрешность измерения расхода ΔQ,
если сопротивление жидкости между электродами R.
5. Записать результат измерения расхода Q.
Решение
Исходные данные сводим в табл. 3.2.
Таблица 3.2
Исходные данные
| Параметр |
Обозначение |
Значение |
| 1. Внутренний диаметр трубопровода, мм |
d |
145 мм |
| 2. Наружный диаметр трубопровода, мм |
D |
150 мм |
|
3. Верхний предел измерения, м3/ч
|
Qmax
|
750 |
| 4. Наибольшее ЭДС, В |
Еmax
|
8,5 |
| 5.Класс точности вольтметра |
|
0,1 |
| 6.Внутреннее сопротивление вольтметра, кОм |
Rv
|
1,1 |
| 7.Сопротивление жидкости между электродами, Ом |
R |
1,2 |
| 8.Показания вольтметра, В |
U |
5 |
3.2.1 Схема индукционного расходомера
Схема турбинного тахометрического расходомера приведена на рис. 3.2.
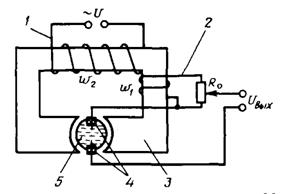
Рис. 3.2. Схема индукционного расходомера
3.2.2 Определение расхода по показанию вольтметра
Расход, соответствующий показанию вольтметра можно определить по формуле
Q=CU (3.1)
где С – цена деления вольтметра, м3/(В·ч)
С=6/4=1,5 м3/(В·ч)
При показании вольтметра U=5 В расход следующий:
Q=1,5·5=7,5 м3/ч
3.2.3 Определение абсолютной погрешности измерения расхода по классу
точности вольтметра
Абсолютная погрешность вольтметра класса точности 0,2 определяем по
формуле
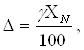 (3.2)
(3.2)
где γ – приведенная погрешность вольтметра, %; XN
- нормирующее значение, В.
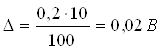
Абсолютная погрешность измерения расхода с учетом цены деления вольтметра
ΔQ=0,02·1,5=0,03 м3/ч
При расходе топлива Q=2,4 В относительная
погрешность измерений составит
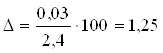 %
%
3.2.4 Определяем погрешность измерения расхода от сопротивления жидкости
между электродами
Так как вольтметр подключается параллельно измерительной цене расходомера,
то
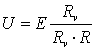 (3.3)
(3.3)
Поэтому при показании вольтметра U=5 В значение
ЭДС в измерительной обмотке
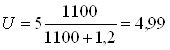 В
В
Расход топлива соответствующий Е=4,99 В определяем по эмпирической
формуле
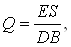 (3.4)
(3.4)
где В – магнитная индукция между полюсами магнита, Тл; S
– площадь поперечного сечения трубопровода, м2.
Создаваемая цепью магнитная индукция – величина постоянная, её можно
определить при наибольших показаниях расходомера:
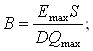 (3.5)
(3.5)
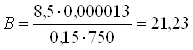
Подставив полученное значение магнитной индукции в формулу, определим
реальный расход топлива с учетом сопротивления жидкости между электродами
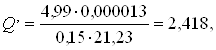
Абсолютная погрешность измерений расхода составит
D = Q – Q’ (3.6)
D=2,4-2,41=0,01 м3/ч
Результат измерения с учетом сопротивления жидкости между электродами и
погрешность вольтметра запишем так:
Q=(2,14±0,03) м3/ч
ЗАДАНИЕ 4. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ СОСТАВА, ВЛАЖНОСТИ И СВОЙСТВ ВЕЩЕСТВ
4.1 Для определения влажности воздуха используется мостовая схема с
термосопротивлениями, измеряющими температуру сухого и влажного воздуха. При
температуре сухого термометра Тс равновесие моста происходит при добавлении
переменного сопротивления Rx.
Требуется:
1. Изобразить схему мостового психрометра.
2. Определить относительную влажность воздуха.
3. Определить погрешность измерения влажности при наличии погрешности
измерения термосопротивления в пределах заданного класса.
Решение
Исходные данные сводим в табл. 4.1.
Таблица 4.1
Исходные данные
| Параметр |
Обозначение |
Значение |
|
1. Температура сухого термометра Тс,
|
Тс
|
14 °С |
| 2. Класс допуска ТС |
В |
- |
|
3. Величина переменного сопротивления Rx,
|
Rx
|
25 Ом |
| 4. Тип термосопротивления |
ТСМ 100 |
- |
4.1.1 Схема мостового психрометра
Схема мостового психрометра приведена на рис. 4.1.
4.1.2 Определяем относительную влажность воздуха
Величина переменного сопротивления определятся по формуле:
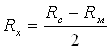 , (4.1)
, (4.1)
где Rс, Rм
– сопротивление сухого и мокрого термосопротивлений.Из формулы (4.1)
получим
Rм = Rс –
2×Rx. (4.2)
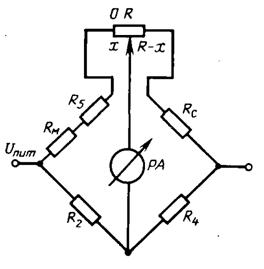
Рис. 4.1. Схема мостового психрометра
При температуре Тс = 14 °С термометр ТСМ 100 будет иметь
сопротивление
Rс =110,65 Ом (см. решение задания
1.3), тогда
Rм =110,65-2·1=108,65,
что соответствует температуре Тм = 20,21ºС
Пользуясь психрометрической таблицей, получим значение относительной
влажности j = 64%
4.1.3 Определяем погрешность измерения влажности при наличии погрешности
измерения термосопротивления в пределах заданного класса
Для класса допуска «В» ТСМ имеем величину погрешности
D= ±(0,25+0,035·Т),%
В нашем случае
Dс = ±(0,25+0,035·25)=1,125%
Dм = ±(0,025+0,035·15)=1,025%
Подставим величины сопротивлений в зависимость (4.1) для получения
наибольшей разности,
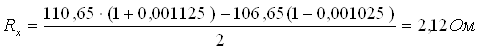
Следовательно, температура с учетом погрешности термосопротивления
составит Тм = 19,7 °С. Таким образом, абсолютная погрешность
измерения температуры мокрым термометром составит
Dм=20,21-19,7=0,5°С
Полученное значение свидетельствует о том, что в данном случае погрешность,
обусловленная классом точности применяемых термосопротивлений, не будет влиять на
точность определения относительной влажности вещества.
Заключение
В результате выполнения расчетной работы были изучены такие важные
вопросы, как
– методы и средства измерения температуры;
– методы и средства измерения давления;
– методы и средства измерения расхода;
– приборы для измерения состава, влажности и свойств веществ.
Также углублены и закреплены знания по дисциплине «Методы и средства
измерений, испытаний и контроля».
Библиографический список
1. О.А. Леонов,
Н.Ж. Шкаруба Курсовое проектирование по метрологии, стандартизации и
сертификации: учебное пособие. – М.
2. Курс лекций
по дисциплине «Методы и средства измерений, испытаний и контроля», доктор
технических наук Леонов О.А.