Реферат: Метод фазового портрета

Иркутская государственная сельскохозяйственная академия

Кафедра информатики и математического моделирования

Реферат на тему:

«Метод фазового портрета»

Выполнил: студент 5курса

агрономического факультета

спец.110102.65

Сароян Д.М.

Проверил: Антонова Н.Н.

Иркутск 2010

Содержание

1.  Фазовый портрет в функционировании реальных сообществ гидробионтов

2.  Типы критических точек на фазовом портрете

3.  Методы построения фазовых портретов

4.  Метод фазовой плоскости

1. Фазовый портрет в функционировании реальных сообществ гидробионтов

В настоящее время в связи с усиливающимся загрязнением водоемов стоит задача обработки первичной экологической информации для мониторинга экосистем и выявления возможных критических ситуаций. Внимание многих экологов обращено на разработку методических подходов, позволяющих использовать для этих целей изменения в сообществах животных. Нарушения в экосистемах можно отнести к важнейшему элементу экологической действительности. Известно, что при отсутствии значимых воздействий наличие отрицательных обратных связей приводит к стабилизации системы. При усилении воздействия на сообщество его структура и функции изменяются, и оно переходит в другое состояние с новыми значениями структурных и функциональных характеристик. При этом наступает момент, когда система не может противостоять воздействию и начинается переход в новое стационарное состояние. Такую точку начала перехода системы из одного устойчивого состояния в другое можно назвать критической точкой.

Разработка методов выявления критических точек позволит ответить на вопрос: когда (в какой год) система не справилась с воздействием? Кроме того, имея информацию о нарастании воздействия, можно оценить величину нагрузки, при которой сообщество гидробионтов выходит из устойчивого состояния. Наличие такой информации крайне важно как для охраны чистоты водоемов, так и для принятия оперативных решений по управлению промыслом рыб.

Перестройки в сообществе при различных воздействиях проходят за определенное время путем последовательных преобразований. Следовательно, его реакция на внешние воздействия в значительной мере обусловлена инерционностью, а само сообщество можно отнести к сложным динамическим системам.

Один из эффективных методов анализа динамической системы состоит в получении ее “фазового портрета” (Волькенштейн, 1978). Он дает возможность выявить стационарные состояния системы и характер ее динамики при отклонении от них. Метод фазовых портретов применяется в технике для анализа и предсказания поведения физических систем различной сложности и в математической экологии для анализа динамики численности популяций (Волькенштейн, 1978; Свирежев, Логофет, 1978).

Для выявления стационарных состояний сообществ гидробионтов использован модифицированный метод структурного фазового портрета (Терещенко, Вербицкий, 1997). Фазовым портретом структуры сообщества является кривая, отражающая поведение системы в координатах H и dH/dt, где H - разнообразие по Шеннону как интегральная структурная характеристика системы. Для исключения влияния случайных изменений проводили сглаживание динамики индекса разнообразия кубическим сплайном.

Существует два отличия использования метода фазовых портретов от того, что было ранее. Во-первых - он не использовался при анализе динамики структуры сообществ, а есть только указание на принципиальную возможность его использования. Во-вторых - ранее фазовые портреты строились на основании уравнений, описывающих эти системы, т.е. на основании моделей. Мы же, основываясь на принципе “любви к объекту исследования”, строили фазовые портреты структуры реальных сообществ на основании исходных данных динамики их разнообразия.

Анализ реакции сообщества основан на поиске стационарных или равновесных состояний. Реально наблюдались стационарные состояния типа: “центр”, “устойчивый фокус” и “неустойчивый фокус”, чему соответствует траектория системы на фазовом портрете в виде цикла, закручивающейся или раскручивающейся спирали (рис. 1).

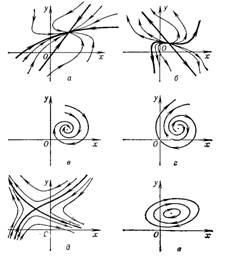
Рис. 1. Фазовые траектории в окрестности особых точек следующих типов: а — устойчивый узел; б — неустойчивый узел; в — устойчивый фокус; г — неустойчивый фокус; д — седло; е — центр.

Проведено изучение поведения реальных биологических сообществ гидробионтов на примере рыбного населения ряда озер и водохранилищ СНГ, а также экспериментальных и природных зоопланктонных сообществ. Показано, что индикатором возмущающего воздействия может служить переход сообщества в другое устойчивое состояние и нарушение плавности кривой фазового портрета.

Анализ структурных фазовых портретов реальных систем в различных экологических ситуациях показал наличие двух типов критических точек в функционировании сообщества.

2. Типы критических точек на фазовом портрете

фазовый портрет сообщество гидробионт

1.  Первый тип критической точки на фазовом портрете представляет собой точку перехода раскручивающейся спирали в дугу. Эта критическая точка соответствует ситуации, когда сообщество уже не может справиться с нарастающим воздействием на него. Из имеющихся данных такой переход в новое состояние отмечен для зоопланктона при влиянии хищника (молоди карпа) на структуру сообщества. Для сообщества рыб такой тип критической точки отмечен при эвтрофировании водоема на примере Сямозера и Мингечаурского водохранилища и влияния техногенной нагрузки на примере озера Имандра.

2.  Второй тип критической точки на фазовом портрете представляет собой точку “перелома” траектории системы и имеет вид нарушений хода кривой в виде пиков. Эта критическая точка соответствует случаю резкого кратковременного возмущающего воздействия на сообщество. При сильном воздействии на водоем происходит элиминация части особей, и отклик на фазовом портрете соответствует по времени действию антропогенного фактора. Подобные изменения на фазовом портрете структуры уловов рыб Рыбинского водохранилища наблюдали в 1984 и 1988 гг., что указывает на резкие возмущающие воздействия на водоем соответственно в 1983 и 1987 гг. Именно в эти годы в водохранилище отмечена массовая гибель рыб. Наиболее сильное влияние на рыб оказала авария на очистных сооружениях г. Череповца в 1987г.

При менее сильных воздействиях ответная реакция проявляется через смертность молоди. Тогда на фазовом портрете отклонения происходят со сдвигом по времени, равным времени вступления молоди в промысел. Такие изменения наблюдались в 1974 году на фазовом портрете структуры уловов рыб Мингечаурского водохранилища. Отмечалось нарушение плавности кривой, что соответствует отклику системы на возмущающее воздействие в 1970 году. В этот год в водохранилище был довольно низкий уровень воды, который обусловил ухудшение условий нереста. В результате в рыбном населении наблюдались небольшие структурные изменения и сдвиг устойчивого состояния на уровень, соответствующий меньшему, чем прежде разнообразию уловов.

Алгоритм выявления критической точки основан на анализе изменения плавности кривой фазового портрета сообщества гидробионтов. Для этого изучалась динамика приращения азимута при перемещении системы по фазовой траектории. Дополнительно анализировалась динамика скорости изменения разнообразия сообщества и его ускорения, которые имеют содержательную биологическую интерпретацию. Скорость изменения разнообразия характеризует интенсивность структурных перестроек, а ускорение, согласно кинематическому аналогу, связано с вызывающими перестройки силами.

В качестве примера критической точки первого типа рассмотрен фазовый портрет рыбного населения озера Имандра. Антропогенное воздействие на водоем увеличивалось с конца 1940-х годов параллельно с развитием металлургических и горно-обогатительных предприятий. Приоритетным фактором воздействия являются тяжелые металлы, а сопутствующим загрязнением - обогащение органическими и биогенными веществами. До 1960-х годов основу улова составляли лососевые и сиговые. В 1970-е годы из промысла практически исчезли крупные кумжа, озерный лосось и крупные сиги. В последнее время в водоеме произошло упрощение структуры рыбной части сообщества, в которой доминируют сиговые, окуневые и карповые.

В 1945-1963 гг. рыбное население водоема находилось в устойчивом состоянии при разнообразии уловов в 2,1 бит. Увеличение воздействия на водоем привело к тому, что к началу 1970-х годов система переходит в новое состояние, соответствующее уровню разнообразия 1.4 бит. 1965 год соответствует времени наступления критической точки в функционировании рыбного населения озера.

Для критических точек первого типа отмечается значительное уменьшение приращений азимута, и даже изменение знака. Скорость и ускорение реагируют на критические точки существенным понижением значений, при этом ускорение (воздействие) опережает изменение скорости (реакция системы). Аналогичные изменения азимута, скорости и ускорения отмечаются и в конце 1970-х годов. Возможно, это связано со сбросом теплых вод с Кольской АЭС, которое началось с 1974 года.

Озеро Имандра представляется интересным объектом для оценки степени воздействия, при которой сообщество рыб выходит из устойчивого состояния. Палеоэкологическая реконструкция антропогенных изменений в озере показывает, что в период 1950-80 годов на озере отмечался линейный рост токсической нагрузки. Наступление критической точки в функционировании рыбного населения озера соответствует 1965-му году. При этом, величина концентрации никеля в донных отложениях равнялась 5 мг/г. Приведенную выше оценку можно рассматривать только в первом приближении, поскольку вопрос о токсической нагрузке на водоем достаточно сложный.

В качестве примера критической точки второго типа рассмотрен фазовый портрет рыбного населения Рыбинского водохранилища. С 1971г. в связи с процессами эвтрофирования и загрязнения водоема в формировании ихтиофауны Рыбинского водохранилища наступил четвертый этап, названный “периодом ухудшения условий” или “дестабилизация”. Возросла амплитуда колебаний уловов рыб и относительной численности отдельных видов, принадлежащих к различным фаунистическим комплексам и экологическим группам. Траектория системы на фазовом портрете имеет вид раскручивающейся спирали, свидетельствующей о ее “разбалансировке” и интенсификации процессов перестройки. Частично это могло быть связано с действием аномально жаркого лета в начале 70-х годов на холодолюбивые виды: снеток и налим. Основной силой, вызвавшей этот процесс, следует считать возрастание в 1970-е годы количества промышленных и сельскохозяйственных стоков, что связано с ростом мощности Череповецкого промышленного узла и увеличением использования удобрений на площади водосбора. Уже в начале 1980-х годов в водохранилище регистрируются случаи локальной гибели рыб.

Для критических точек второго типа отмечается кратковременный всплеск абсолютных значений приращений азимута. Скорость и ускорение реагируют на критические точки существенным одновременным понижением значений.

Таким образом, предложен алгоритм выявления критической точки на основании анализа изменения плавности кривой фазового портрета сообщества гидробионтов. В основе алгоритма лежит изучение динамики приращения азимута при перемещении системы по фазовой траектории. Показано, что в критических точках происходит существенное изменение приращения азимута. При этом каждому типу критической точки соответствует свой тип изменения угла.

В дальнейшем стоит задача создания на основе этого алгоритма информационно-экспертной системы оценки экологической ситуации в водоемах.

3. Методы построения фазовых портретов

Для построения фазовых портретов можно использовать различные методы: метод дифференциальных уравнений, метод изоклин, и др.

Метод дифференциальных уравнений. Сущность метода заключается в том, что по дифференциальным уравнениям отдельных участков нелинейного элемента строят соответствующие фазовые портреты на плоскости.

Метод изоклин - это метод линий постоянного наклона.

4. Метод фазовой плоскости

графоаналитический метод исследования динамических систем, описываемых уравнениями вида:

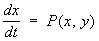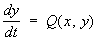 ,  , где х и у – переменные состояния системы,

Р (х, у) и Q (х, у) – функции, удовлетворяющие условиям теорем существования и единственности решений, t – время (независимая переменная). Поведение такой системы можно представить геометрически на плоскости в прямоугольных декартовых координатах. При таком представлении каждому состоянию динамической системы однозначно соответствует точка на плоскости с координатами х, у и, наоборот, каждой точке плоскости соответствует одно, и только одно состояние исследуемой динамической системы. Плоскость Оху называется фазовой плоскостью. Изменение состояния системы отображается на фазовой плоскости движением точки, которую называют фазовой, изображающей или представляющей точкой. Траектория, по которой движется изображающая точка, называется фазовой траекторией; скорость и направление её движения определяются вектором фазовой скорости {Р, Q}. Существенно, что через каждую точку фазовой плоскости проходит только одна фазовая траектория. Совокупность фазовых траекторий называется фазовым портретом системы и отображает совокупность всех возможных сочетаний системы и типы возможных движений в ней.

На фазовой плоскости обычно выделяют следующие три типа фазовых траекторий: особые точки, или положения равновесия, определяемые в результате решения системы уравнений

Р (х, у) = 0, Q (х, y) = 0;

изолированные замкнутые траектории, отвечающие периодическим движениям в системе; сепаратрисы, разделяющие фазовую плоскость на области, заполненные траекториями разных типов. Ф. п. м. состоит в построении фазового портрета системы и последующего анализа этого портрета.