Учебное пособие: Фізичні основи електроніки
МІНІСТЕРСТВО
ОСВІТИ І НАУКИ УКРАЇНИ
УЖГОРОДСЬКИЙ
НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
НЖЕНЕРНО-ТЕХНІЧНИЙ
ФАКУЛЬТЕТ
КАФЕДРА
ПРИЛАДОБУДУВАННЯ
ФІЗИЧНІ ОСНОВИ
ЕЛЕКТРОНІКИ
Методичні вказівки до виконання
лабораторних робіт
Ужгород–2008
Фізичні основи
електроніки. Методичні
вказівки до виконання лабораторних робіт. Ужгород, 2006. –47с.
Приведено короткі
теоретичні відомості, хід роботи та методику обробки експериментальних
результатів при виконанні лабораторних з курсу “Фізичні основи електроніки”.
Укладачі:
Козусенок О. В. старший
викладач кафедри приладобудування
Федак В. В., кандидат
фізико–математичних наук, доцент кафедри приладобудування
Рецензенти:
Бутурлакін О. П. кандидат
фізико–математичних наук, доцент кафедри приладобудування
Онопко В.В.
кандидат фізико–математичних наук, доцент кафедри електронних систем
Відповідальний за випуск:
Туряниця І. І.,
кандидат фізико–математичних наук, доцент, завідувач кафедри приладабудування
Затверджено на
засіданні кафедри приладобудування
14 лютого 2007
року протокол №4
_____________________________________________________________
© Козусенок О.
В., Федак В. В., 2008
ЗМІСТ
ВСТУП
ЛАБОРАТОРНА РОБОТА №1. Вивчення
основних закономірностей тліючого розряду
ЛАБОРАТОРНА РОБОТА №2. Вивчення
термоелектронної емісії
ЛАБОРАТОРНА РОБОТА №3. Дослідження
основних властивостей внутрішнього фотоефекту
ЛАБОРАТОРНА РОБОТА №4. Дослідження
впливу електричного поля на електропровідність напівпровідників
ЛАБОРАТОРНА РОБОТА №5.
Експериментальне вивчення ємнісних властивостей p–n
переходів
ЛАБОРАТОРНА РОБОТА №6. Дослідження
впливу температури на вольт–амперну характеристику p–n переходу
ЛАБОРАТОРНА РОБОТА №7. Дослідження
механізмів пробою p–n переходів
ДОДАТОК №1
Спектральний розподіл густини
випромінювання абсолютно чорного тіла
ДОДАТОК №2
Властивості власних напівпровідників Si, Ge і GaAs при 300 К
ВСТУП
Курс “Фізичні основи електроніки” читається студентам
інженерно–технічного факультету, які навчаються на спеціальностях “Наукові,
аналітичні і екологічні прилади та системи” та “Електронні системи”. Завдання
цього курсу – дати студентам теоретичну базу в області фізичної електроніки,
яка дозволить їм успішно засвоїти такі курси як “Електронні прилади”, “Основи
сенсорної електроніки”, схемотехнічні дисципліни електроніки та ін.
В цей методичний
посібник ввійшли описи лабораторних робіт в яких проводяться дослідження
базових явищ та ефектів, що лежать в основі роботи значної кількості
електронних приладів. Сюди не включені лабораторні роботи, які виконуються з
курсу загальної фізики і описані в методичному посібнику [1].
Теоретичні
відомості, приведені до лабораторних робіт не претендують на повноту викладу
теоретичних аспектів досліджуваних явищ. Вони дають тільки мінімальну
інформацію, яка необхідна для обробки експериментальних результатів. Для більш
повного осмислення необхідно вивчити матеріал, який приведений у переліку основних
теоретичних питань. Приведені у додатках відомості про основні властивості
власних напівпровідників Si, Ge і GaAs використовуються при аналізі та
обробці експериментальних результатів.
При постановці лабораторних робіт та підготовці посібника
використано досвід кафедри фізики напівпровідників у постановці лабораторних по
курсу “Фізика напівпровідників” та відповідні технологічні карти [2].
Автори будуть вдячні за внесені конструктивні
пропозиції відносно змісту та форми даного методичного посібника.
ЛАБОРАТОРНА РОБОТА №1
Вивчення основних
закономірностей тліючого розряду
Мета роботи:
освоєння методики дослідження вольт–амперної характеристики (ВАХ) тліючого
розряду та вивчення умов стабільності розряду.
Необхідні прилади
і матеріали: неонова лампа типу ТН-0,3-3, блок живлення з регульованою напругою
0 – 120 В, вольтметр, мілі-, та мікро-амперметр.
Теоретичні
питання знання, яких необхідне для виконання лабораторної роботи:
1. Типи газового розряду.
2. Умова
виникнення газового розряду. Ефект лавинного помноження.
3. Ефект газового
підсилення. Умови стабільності газового розряду.
4. Використання
газового розряду.
Основні теоретичні відомості
та методика експерименту
Проходження електричного струму через газ
називають електричним розрядом у газі або газовим розрядом. Гази, на відміну від металів і електролітів при
нормальних умовах складаються з електрично нейтральних атомів і молекул і тому
є добрими ізоляторами. Щоб зробити газ провідним, треба певним чином створити в
ньому або внести вільні носії заряду. Це можливо зробити шляхом іонізації
атомів і молекул газу. Іонізація відбувається під дією космічного ,
рентгенівського та радіоактивного випромінювань, при бомбардуванні атомів або
молекул газу швидкими електронами, при нагріванні та інших факторів.
Електричні розряди в газі поділяються на
несамостійні і самостійні.
Несамостійним називають газовий розряд, для підтримання якого необхідна
емісія електронів з катода або утворення заряджених частинок у розрядному
проміжку під дією зовнішніх факторів, з припиненням їх дії розряд зникає.
Розглянемо несамостійний розряд кількісно. Для спрощення вважатимемо:
–
розряд відбувається між двома плоскими електродами;
–
концентрація позитивних і негативних зарядів
однакова, тобто 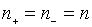 ;
;
–
заряди позитивних і негативних іонів по абсолютній
величині рівні і дорівнюють заряду електрона |q|.
Повна густина струму при наявності дифузійних потоків буде визначатися
виразом
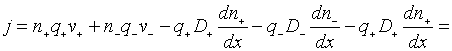
=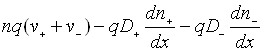 ,
(1.1)
,
(1.1)
де 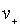 ,
,
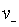 ,
, 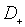 ,
, 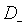 – відповідно
швидкості напрямленого руху і коефіцієнти дифузії позитивних і негативних
іонів. Якщо концентрація іонів у всьому об’ємі між електродами та сама, то
дифузійних потоків іонів не буде. Тоді вираз (1.1) перепишемо так:
– відповідно
швидкості напрямленого руху і коефіцієнти дифузії позитивних і негативних
іонів. Якщо концентрація іонів у всьому об’ємі між електродами та сама, то
дифузійних потоків іонів не буде. Тоді вираз (1.1) перепишемо так:
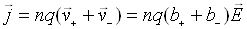 ,
(1.2)
,
(1.2)
де b+, b–
– рухливості іонів газу; 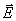 – напруженість електричного поля.
Формула (1.2) подібна до закону Ома для густини струму. Вона буде еквівалентна
цьому закону, якщо множник
– напруженість електричного поля.
Формула (1.2) подібна до закону Ома для густини струму. Вона буде еквівалентна
цьому закону, якщо множник 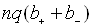 не залежить від
не залежить від  .
.
Запишемо рівняння балансу іонів у газі при наявності в ньому
електричного струму і постійної дії зовнішнього іонізатора. Нехай під дією
іонізатора щосекунди в одиниці об’єму утворюється 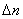 пар іонів. Внаслідок рекомбінації
іонів щосекунди зникає в одиниці об’єму певна кількість пар іонів
пар іонів. Внаслідок рекомбінації
іонів щосекунди зникає в одиниці об’єму певна кількість пар іонів 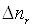 , яка
пропорційна як концентрації позитивних іонів n+, так і концентрації негативних іонів n–, тобто
, яка
пропорційна як концентрації позитивних іонів n+, так і концентрації негативних іонів n–, тобто 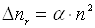 (α –
коефіцієнт рекомбінації, n+=n–=n). При наявності
електричного струму також відбувається зменшення концентрації іонів газу. Якщо
площа електрода S, а відстань між
електродами l, то при силі струму
І (густині струму j) зменшення
кількості іонів в одиниці об’єму за одиницю часу визначається
(α –
коефіцієнт рекомбінації, n+=n–=n). При наявності
електричного струму також відбувається зменшення концентрації іонів газу. Якщо
площа електрода S, а відстань між
електродами l, то при силі струму
І (густині струму j) зменшення
кількості іонів в одиниці об’єму за одиницю часу визначається
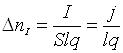 .
.
Рівняння балансу матиме вигляд
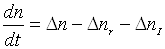 ,
або
,
або 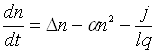 . (1.3)
. (1.3)
умовою рівноваги при наявності струму є 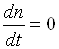 , тобто
, тобто
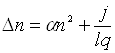 .
(1.4).
.
(1.4).
Розглянемо такі випадки. Якщо густина струму незначна, тобто 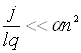 , то
, то 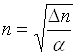 і вираз (1.2)
матиме вигляд
і вираз (1.2)
матиме вигляд
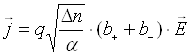 .
(1.5)
.
(1.5)
Цей випадок реалізується при досить малих напруженостях електричного
поля  . Для
таких полів виконується закон Ома в газових розрядах.
. Для
таких полів виконується закон Ома в газових розрядах.
У другому випадку вважатимемо, що зменшенням концентрації іонів за
рахунок їхньої рекомбінації можна нехтувати порівняно з зменшенням концентрації
іонів за рахунок наявності електричного струму, тобто 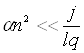 . Тоді
. Тоді
 . (1.6)
. (1.6)
Звідси видно, що за такої умови густина струму не залежить від
напруженості  . Формула (1.6) виражає густину
струму насичення. Величина j
залежить від Δn, тобто від
іонізуючої здатності іонізатора.
. Формула (1.6) виражає густину
струму насичення. Величина j
залежить від Δn, тобто від
іонізуючої здатності іонізатора.
З формули (1.6) випливає дещо несподіваний на перший погляд висновок
про те, що густина струму насичення j тим більша, чим більша відстань між
електродами. Цей висновок справедливий за умови, якщо іонізація відбувається в
усьому об’ємі між електродами. Оскільки при струмі насичення кількість іонів,
що утворюється за одиницю часу, дорівнює кількості іонів, які щосекунди
досягають електродів, тому відповідно і густина струму пропорційна l, бо при більшій відстані між електродами
виникатиме більша кількість іонів. Для проміжних значень напруженості
електричного поля залежність сили струму від напруженості має складніший
характер, тобто закон Ома не виконується.
У цьому випадку, при підвищенні напруги сила струму розряду різко
зростає в сотні і тисячі разів. Дослід показує, що при припинені дії іонізатора
струм не змінюється. Такий розряд у газах називають самостійним.
Самостійним
називають електричний розряд, для підтримання якого не потрібне утворення
заряджених частинок під дією зовнішніх факторів. При самостійному розряді
генерація і рух зарядів у розрядному проміжку здійснюється тільки за рахунок
енергії електричного поля, яке діє між електродами – катодом і анодом.
Якщо електрон,
який рухається в електричному полі до анода набуває енергії достатньої для
іонізації атомів (молекул) газу при непружному зіткненні, то виникають
позитивний іон і новий електрон. При наступному непружному співударі
утворюється нова пара носіїв заряду і т. д. Такий процес виникнення електронів
та іонів називають електронною або іонною лавиною.
Для розгляду
цього процесу кількісно позначимо через α кількість пар іонів, що
утворюються внаслідок непружного удару з атомами газу на одиниці довжини шляху.
Тоді збільшення густини потоку електронів, що виникає в шарі товщиною dx, виражається співвідношенням
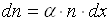 , (1.7)
, (1.7)
де n – густина потоку електронів, що
входять у перпендикулярному напрямі до поверхні уявно виділеного шару товщиною dx на відстані x від катода. Якщо вважати, що утворення
нових пар електронів і іонів не приводить до істотних змін електричного поля у
між електродному просторі, то
коефіцієнт α можна вважати сталим для даного процесу.
Інтегруючи (1.7),
отримуємо
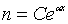 , (1.8)
, (1.8)
де С – стала
інтегрування. При x=0 величина n дорівнює кількості електронів, що
вивільнюються з одиниці площі катода під дією зовнішнього іонізатора, тобто n=n0.
Отже, С=n0. Тоді
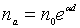 . (1.9)
. (1.9)
Звідси
випливає, що тільки при ударній іонізації розряд не може бути самостійним,
оскільки при n0=0 nа також дорівнює нулю. Щоб розряд був
самостійним, треба, щоб електронні лавини підтримували самі себе, тобто у газі
має відбуватись ще один процес, у результаті якого утворювалися б нові
електрони. Одним з таких процесів може бути вторинна електронна емісія з катода
при бомбардуванні його іонами. Позначимо кількість електронів, що вивільняються
з катода під дією зовнішнього іонізатора і внаслідок вторинної електронної
емісії, через nк. тоді густина потоку електронів на аноді буде
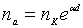 . (1.10)
. (1.10)
Внаслідок
ударної іонізації електронів, кількість електронів, що виникає в лавині,
дорівнює кількості позитивних іонів, які при цьому утворюються, тобто
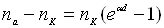 . (1.11)
. (1.11)
При
бомбардуванні катода іонами внаслідок вторинної електронної емісії з нього
вивільнятиметься електронів 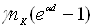 , де γ – коефіцієнт
пропорційності (для металів γ<1). Тоді, враховуючи одночасну дію
зовнішнього іонізатора і вторинну електронну емісію з катода, можна записати,
що
, де γ – коефіцієнт
пропорційності (для металів γ<1). Тоді, враховуючи одночасну дію
зовнішнього іонізатора і вторинну електронну емісію з катода, можна записати,
що
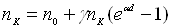 . (1.12)
. (1.12)
Звідси
маємо
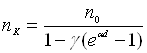 . (1.13)
. (1.13)
Тоді
густина потоку електронів на аноді
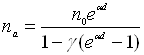 . (1.14)
. (1.14)
Оскільки
на аноді струм газового розряду повністю визначається рухом електронів, то
густина струму на основі (1.14) виражатиметься так:
 . (1.15)
. (1.15)
При
стаціонарному режимі розряду густина струму повинна бути однакова у всьому
проміжку газового розряду, тому густина струму складатиметься з суми густин
електронного je і іонного струмів ji , тобто
j=je +ji.
Аналіз
виразу (1.15) свідчить про те, що за умови, коли
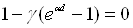 , густина струму
, густина струму 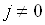 навіть при припиненні
дії зовнішнього іонізатора
навіть при припиненні
дії зовнішнього іонізатора 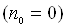 . Отже, умовою виникнення
самостійного розряду є рівність
. Отже, умовою виникнення
самостійного розряду є рівність
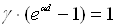 . (1.16)
. (1.16)
напруга
при якій виконується умова (1.16), називається напругою запалювання газового
розряду.
Електрони
для підтримання електронної лавини можуть утворюватись не тільки ударною
іонізацією електронами, можлива іонізація атомів та молекул іонами та
фотоіонізацією. Крім цього необхідно врахувати і неоднорідність електричного
поля, яке зумовлене об’ємними зарядами при іонізації газу. Все це вказує на
складність газового розряду. Тому єдиної теорії самостійного газового розряду,
яка враховувала б усі процеси, ще не створено.

Рис. 1.1
Принципова електрична схема включення розрядної трубки при дослідженні газового розряду
Якщо розрядну
трубку з двома електродами, наповнену газом, ввімкнути в електричне коло з
джерелом високої напруги GB1 і баластним резистором R1, який дає можливість
регулювати струм у колі (рис. 1.1), то залежно від величини струму через
газовий проміжок в ньому виникнуть різні види електричного розряду, які
відрізняються фізичними процесами в об’ємі газу і на електродах, характером
свічення і величиною спаду напруги Ua між електродами.
На рис. 1.2 приведена типова залежність спаду напруги на газорозрядній
лампі від величини струму, яка називається вольт-амперною характеристикою
газового розряду. Ділянка 0а відповідає несамостійному темному розряду, а
ділянка ab – самостійному темному
розряду.
Вертикальна
ділянка cd, відповідає нормальному
тліючому розряду. При подальшому збільшенню струму в трубці спостерігається
аномальний тліючий розряд (ділянка de). При
струмах від одиниць до сотень і тисяч ампер виникає дуговий розряд (ділянка fg). Ділянки bc і ef відповідають нестійким перехідним
розрядам – від темного до тліючого і від аномального тліючого до дугового.
Завдання до лабораторної роботи
1. Зібрати схему, зображену на рис. 1.1.
2. Дослідити ВАХ неонової лампи.
3. Побудувати ВАХ і визначити:
а) потенціал U3 і струм запалювання розряду (І3=Іа);
б) напругу
горіння UГ та діапазон струмів тліючого розряду
при цьому;
в) вказати
ділянки самостійного та несамостійного розрядів;
г) для кожної
ділянки ВАХ визначити величини диференціальних опорів:
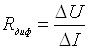 .
.
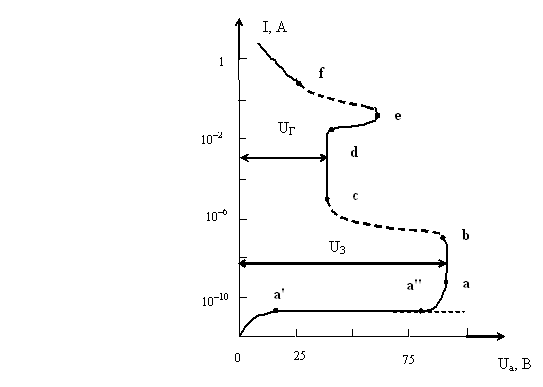
Рис. 1.2
Вольт-амперна характеристика електричного розряду у газі
4. Оцінити
похибку вимірювань та зробити висновки
Література
[1]. c. 370-400. [2]. c. 322-339. [3]. c. 185-215.
ЛАБОРАТОРНА РОБОТА №2
Вивчення
термоелектронної емісії
Мета роботи:
експериментальна перевірка формули Річардсона-Дешмана, закону 3/2 та визначення
термоелектронної роботи виходу.
Необхідні прилади
і матеріали: джерело постійної напруги (0÷5 В; 0÷100 В),
вольтметри постійного струму (1 В; 100 В); омметр; електровакуумні діоди з
катодами прямого розжарення.
Теоретичні
питання знання, яких необхідне для виконання лабораторної роботи:
1. Потенціальний бар’єр на границі твердого тіла.
2. Явище
термоелектронної емісії (ТЕ). ТЕ металів та напівпровідників.
3. Вплив
зовнішнього електричного поля на ТЕ металів.
4. ТЕ при
наявності на поверхні металу моноатомного шару адсорбованої речовини.
5. Оксидний
катод.
Основні
теоретичні відомості та методика експерименту
Емісію
електронів, яка виникає в результаті нагріву тіл, називають термоелектронною
емісією. Явище ТЕ широко використовують у вакуумних і газонаповнених приладах.
Кількісні та якісні співвідношення, які визначають струм емісії IS від параметрів матеріалу
катоду і його температури Т, задаються формулою Річардсона-Дешмана:
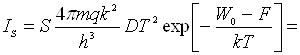
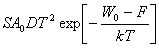 , (2.1)
, (2.1)
де константа 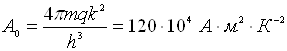 є
універсальною і не залежить від роду емітера;
є
універсальною і не залежить від роду емітера; 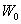 – робота, яку необхідно виконати
для переводу електрона з будь-якого енергетичного рівня на рівень вакууму;
– робота, яку необхідно виконати
для переводу електрона з будь-якого енергетичного рівня на рівень вакууму; 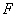 – енергія
Фермі; D – середній коефіцієнт
прозорості потенціального бар’єру (як правило D≈1); S – ефективна площа катода.
– енергія
Фермі; D – середній коефіцієнт
прозорості потенціального бар’єру (як правило D≈1); S – ефективна площа катода.
Замінивши в
рівнянні (2.1) різницю 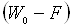 ефективною роботою виходу, яка є
параметром даного матеріалу і визначає його термоемісійні властивості рівняння
Річардсона-Дешмана можна записати у більш поширеному вигляді:
ефективною роботою виходу, яка є
параметром даного матеріалу і визначає його термоемісійні властивості рівняння
Річардсона-Дешмана можна записати у більш поширеному вигляді:
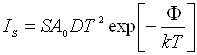 , (2.2)
, (2.2)
де Ф –
термоелектронна робота виходу.
Вирази (2.1) і (2.2) є основним законом термоелектронної емісії. Вони
характеризують залежність струму емісії від температури і термодинамічної
роботи виходу. Видно, що при збільшенні температури струм зростає по
експоненціальному закону, аналогічна залежність має місце при зменшенні роботи
виходу.
Залежність (2.2) зручно представляти у логарифмічному масштабі від
оберненої температури. Дійсно, так як
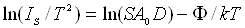 ,
(2.3)
,
(2.3)
то функція в координатах 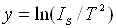 і
і  є рівнянням прямої
є рівнянням прямої 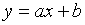 , кутовий коефіцієнт
якої
, кутовий коефіцієнт
якої 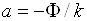 , а
точка її перетину з віссю ординат –
, а
точка її перетину з віссю ординат – 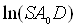 .
.
Цю властивість зручно використовувати для експериментального визначення
термодинамічної роботи виходу. Знайдемо значення струмів емісії при двох
температурах:
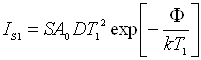 ,
,
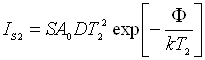 .
.
Якщо прологарифмувати і від першого рівняння відняти друге, то одержимо
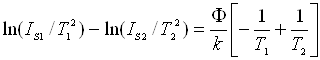 .
.
Звідси
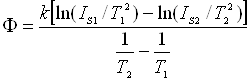 .
(2.4)
.
(2.4)
У цій лабораторній роботі досліджуються анодні характеристики
електровакуумного діода з катодом прямого нагріву який являє собою тонку
дротину з тугоплавкого металу, який нагрівається безпосередньо струмом, що проходить
через неї. Схема включення експериментальної лампи для визначення емісійних
констант катода зображена на рис. 2.1.
Анодною характеристикою діода називають залежність 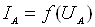 при постійній напрузі
розжарювання (
при постійній напрузі
розжарювання (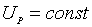 ).
).
Найбільш проста теоретична залежність 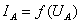 одержується в одномірному
наближенні для плоскої системи електродів, коли катод і анод являють собою дві
плоскі паралельні пластини необмежених розмірів віддаль між якими rA . приймемо, що потенціал UK=0, а анода U=UA. Будемо також вважати, що електрони покидають катод з нульовою
швидкістю, тобто v0=0. Вихідну
систему рівнянь запишемо у наступному вигляді:
одержується в одномірному
наближенні для плоскої системи електродів, коли катод і анод являють собою дві
плоскі паралельні пластини необмежених розмірів віддаль між якими rA . приймемо, що потенціал UK=0, а анода U=UA. Будемо також вважати, що електрони покидають катод з нульовою
швидкістю, тобто v0=0. Вихідну
систему рівнянь запишемо у наступному вигляді:
 ;
; 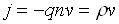 ;
; 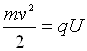 , (2.5)
, (2.5)
де U – потенціал; 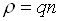 – густина
об’ємного заряду; m, q, n, v – відповідно маса, заряд, концентрація і швидкість електронів;
– густина
об’ємного заряду; m, q, n, v – відповідно маса, заряд, концентрація і швидкість електронів; 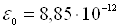 Ф/м; j – густина струму.
Ф/м; j – густина струму.
Перший вираз в системі (2.5) – рівняння Пуассона, другий – рівняння
неперервності, третій – рівняння руху. Алгоритм розв’язку системи рівнянь (2.5)
наступний: з рівняння руху знаходяться швидкість v і підставляється у рівняння неперервності, звідки знаходиться густина 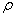 і
підставляється у рівняння Пуассона, яке потім двічі інтегрується з врахуванням
початкових умов (x=0, U=UK=0, EK=0, v0=0; x=rA, U=UA). Після виконання вказаних
операцій одержимо
і
підставляється у рівняння Пуассона, яке потім двічі інтегрується з врахуванням
початкових умов (x=0, U=UK=0, EK=0, v0=0; x=rA, U=UA). Після виконання вказаних
операцій одержимо
 .
(2.6)
.
(2.6)
Анодний струм IA=SA∙j,
де SA – ефективна поверхня анода. Якщо SA
– це та частина поверхні анода, на яку попадають електрони, тоді
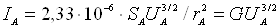 ,
(2.7)
,
(2.7)
де G=2,33∙10-6SA/ 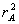 – постійна
величина для кожної конкретної лампи.
– постійна
величина для кожної конкретної лампи.
Вираз (2.7) називають законом трьох других. Якщо конструкція приладу
відрізняється від плоскої, то у вираз (2.7) вводять спеціальні коефіцієнти,
значення яких не більше одиниці і які залежать від конструкції електродів.
Закон степені трьох других справедливий тільки для режиму об’ємного заряду. В
режимі насичення струм анода ідеального діода рівний струму емісії IS і не
залежить від UA.
На рис. 2.2 приведена анодна характеристика реального діода. Як видно
насичення анодного струму є неповним. Це зумовлено дією прискорюючого
електричного поля біля поверхні катода. Цей ефект називають ефектом Шотткі, а
ВАХ діода у цьому випадку описується наступним рівнянням (рівняння Шотткі):
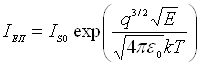 ,
(2.8)
,
(2.8)
де ІS0 струм емісії при відсутності електричного поля, Е – напруженість
електричного поля.
Прологарифмувавши (2.8) і врахувавши, що 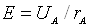 , одержуємо
, одержуємо
 .
(2.9)
.
(2.9)
Таким чином графік залежності логарифма струму діода від кореня
квадратного анодної напруги представляє собою пряму лінію, яка відсікає по осі
ординат відрізок, рівний логарифму струму емісії при відсутності поля. Це дає
можливість більш точно визначити цю величину, ніж по злому ВАХ.
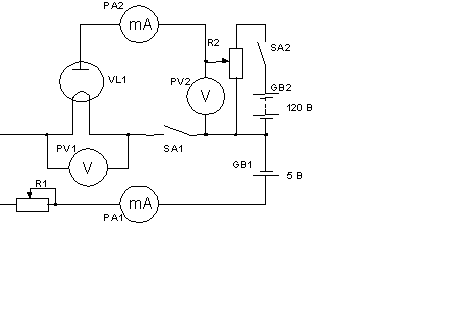
Рис. 2.1 Принципова електрична схема для дослідження термоелектронної
емісії

Рис. 2.2 Анодна характеристика реального діода
Завдання до лабораторної роботи
1. Зібрати електричну схему, зображену на рис.
2.1.
2. За допомогою омметра виміряти опір катода
при кімнатній температурі.
3. Дослідити ВАХ діода при різних значеннях
струмів катода (не менше 5 значень).
4. Побудувати ВАХ
ІА=f(UA) та вказати на них область дії
об’ємного заряду.
5. Для одного з
значень струму катода перевірити виконання закону трьох других та визначити
постійну лампи G.
6. Для анодних напруг де ІА
виходить на насичення, побудувати залежності 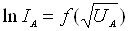 . Шляхом екстраполяції до UA=0 визначити значення струму
термоелектронної емісії IS.
. Шляхом екстраполяції до UA=0 визначити значення струму
термоелектронної емісії IS.
7. Виходячи з
формули 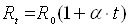 ,
знайти температуру катода (t – температура в ˚С, α – температурний коефіцієнт опору
матеріалу катода – вольфраму).
,
знайти температуру катода (t – температура в ˚С, α – температурний коефіцієнт опору
матеріалу катода – вольфраму).
8. Побудувати
залежності 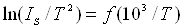 .
За тангенсом кута нахилу цієї залежності визначити ефективну термоелектронну
роботу виходу.
.
За тангенсом кута нахилу цієї залежності визначити ефективну термоелектронну
роботу виходу.
9. Обчислити
похибки вимірювань. Порівняти одержані результати з літературними даними для
матеріалу катода. Зробити висновки.
Література
[1]. c. 248-278. [2]. c. 192-207. [3]. c. 151-166. [4]. с. 270–273.
ЛАБОРАТОРНА РОБОТА №3
Вивчення
фотопровідності напівпровідників
Мета роботи:
загальне ознайомлення з методикою дослідження фотоелектричних властивостей
напівпровідників і вимірювання спектральної залежності фотопровідності і
люксамперних характеристик та визначення основних параметрів
напівпровідникового матеріалу.
Необхідні прилади
і матеріали: напівпровідниковий фоточутливий елемент; монохроматор; джерело
світла; джерело постійної напруги; мікроамперметр; нейтрально сірі
світлофільтри.
Теоретичні питання знання, яких
необхідне для виконання лабораторної роботи:
1. Основні закони теплового випромінювання.
Формула Планка.
2. Механізми
поглинання світла в напівпровідниках.
3. Рівноважні та нерівноважні носії заряду.
Статистика нерівноважних носіїв заряду.
4. Фотопровідність – власна та домішкова.
Спектральна залежність фотопровідності. Релаксація фотопровідності.
5. Рекомбінація нерівноважних носіїв заряду –
випромінювальна та безвипромінювальна. Рекомбінація через домішковий рівень.
Основні теоретичні відомості та
методика експерименту
Внутрішній фотоефект – це процес внутрішньої іонізації напівпровідника
під дією світла, який приводить до утворення додаткових, нерівноважних носіїв
заряду. Додаткову провідність, зумовлену внутрішнім фотоефектом, називають
фотопровідністю.
При внутрішньому фотоефекті первинним процесом є поглинання фотона з
енергією, достатньою для збудження електрона в зону провідності (переходи 1 і
2, рис.3.1), або на локальні рівні енергії (перехід 3, рис.3.1), розташовані в
забороненій зоні напівпровідника. Перехід 1 приводить до утворення пари
електрон – дірка, тоді як у результаті переходів 2 і 3 утворюються носії заряду
тільки одного знаку.
Якщо оптичне збудження електронів відбувається з валентної зони в зону
провідності, то спостерігається власна фотопровідність, яку створюють носії
обох знаків. При цьому, очевидно, енергія фотона hν має бути не менша ширини забороненої зони напівпровідника 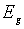 (
( ). Нерівноважні електрони й дірки, утворені в
результаті взаємодії з фотонами достатньо великих енергій, одразу після процесу
іонізації можуть мати енергію, яка є значно більшою чим середня теплова енергія
теплового руху рівноважних носіїв заряду, яка по порядку величини близька до kT. Але в результаті взаємодії з фононами та
дефектами кристалічної ґратки нерівноважні носії заряду швидко набувають
температуру ґратки і їх енергія стає рівною середній тепловій енергії
рівноважних носіїв заряду.
). Нерівноважні електрони й дірки, утворені в
результаті взаємодії з фотонами достатньо великих енергій, одразу після процесу
іонізації можуть мати енергію, яка є значно більшою чим середня теплова енергія
теплового руху рівноважних носіїв заряду, яка по порядку величини близька до kT. Але в результаті взаємодії з фононами та
дефектами кристалічної ґратки нерівноважні носії заряду швидко набувають
температуру ґратки і їх енергія стає рівною середній тепловій енергії
рівноважних носіїв заряду.
Цей процес відбувається за час порядку 10-10с, який
називають часом релаксації носіїв струму. Як правило, час життя τ
нерівноважних носіїв значно перевищує цю величину і складає 10-2–10-7с
і, відповідно, більшу частину часу до рекомбінації їх кінетична
|
енергія відповідає середній
тепловій енергії рівноважних носіїв заряду. Тому можна вважати, що розподіл
по енергіях нерівноважних носіїв заряду в зонах є таким самим, як для рівно      важних. важних.
|
ЕС
2
Едом
1 3
ЕV
Рис. 3.1 Схема можливих оптичних
переходів електронів в забороненій зоні
|
Значить і рухливості μ нерівноважних носіїв не відрізняється від
рухливості рівноважних, так як рухливості електронів 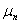 і дірок
і дірок 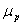 визначаються характером взаємодії
носіїв заряду з ґраткою і залежать, зокрема, від розподілу носіїв заряду по
енергіях.
визначаються характером взаємодії
носіїв заряду з ґраткою і залежать, зокрема, від розподілу носіїв заряду по
енергіях.
Таким чином, генерація носіїв заряду під дією світла приводить до зміни
електропровідності σ напівпровідника, яка при наявності нерівноважних
електронів і дірок з концентраціями Δn та Δp, відповідно, може бути записана у
наступному вигляді
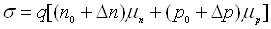 ,
(3.1)
,
(3.1)
де 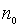 і
і
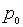 –
концентрації рівноважних електронів і дірок.
–
концентрації рівноважних електронів і дірок.
Надлишкова (нерівноважна) провідність, рівна різниці провідностей
напівпровідника при наявності (σ) і при відсутності (σ0)
освітлення представляє собою фотопровідність (σф):
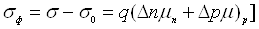 .
(3.2)
.
(3.2)
Природно, що концентрації нерівноважних носіїв Δn і Δp залежать від інтенсивності і
тривалості освітлення напівпровідника.
Позначимо
швидкість генерації носіїв заряду під дією освітлення 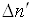 і
і 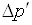 . Очевидно, що
. Очевидно, що 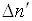 і
і 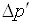 мають бути пропорційні
світловій енергії, яка поглинається за одиницю часу в одиниці об’єму
напівпровідника. Якщо інтенсивність монохроматичного в шарі напівпровідника
товщиною dx рівна J, а коефіцієнт поглинання світла
рівний α, то кількість світлової енергії, поглинутої за одиницю часу в
одиниці об’єму, рівна:
мають бути пропорційні
світловій енергії, яка поглинається за одиницю часу в одиниці об’єму
напівпровідника. Якщо інтенсивність монохроматичного в шарі напівпровідника
товщиною dx рівна J, а коефіцієнт поглинання світла
рівний α, то кількість світлової енергії, поглинутої за одиницю часу в
одиниці об’єму, рівна:
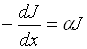 . (3.3)
. (3.3)
Таким чином,
швидкість генерації носіїв 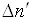 і
і 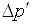 пропорційна величині αJ. Для області фундаментального
поглинання
пропорційна величині αJ. Для області фундаментального
поглинання
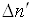 =
=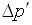 =βαJ. (3.4)
=βαJ. (3.4)
Коефіцієнт
пропорційності β називають коефіцієнтом квантового виходу, так як він
визначає число пар носіїв заряду (або число носіїв заряду при монополярній
генерації), які утворюються в результаті поглинання одного кванта світла, якщо
інтенсивність світла J вимірювати
числом квантів за секунду. За звичай коефіцієнт квантового виходу β не
перевищує одиниці.
При неперервному
освітленні напівпровідника світлом постійної інтенсивності встановлюється
стаціонарний стан, який характеризується постійними концентраціями
нерівноважних носіїв заряду Δn і Δp. Знайдемо залежність Δn і Δp від часу t і визначимо стаціонарні значення концентрацій нерівноважних носіїв
заряду, вважаючи інтенсивність світла постійною у всьому об’ємі зразка, що
приводить до однорідної генерації носіїв заряду.
Одразу після
початку освітлення, по мірі збільшення концентрації нерівноважних носіїв заряду
починає зростати інтенсивність процесу рекомбінації. Оскільки швидкість
генерації нерівноважних залишається постійною при постійній інтенсивності
освітлення, то інтенсивність процесу рекомбінації швидко досягає інтенсивності
процесу генерації носіїв, і встановлюється стаціонарний стан нерівноважної
концентрації фотоносіїв.
Зміна концентрації
нерівноважних носіїв за одиницю часу є різниця між швидкостями генерації і
рекомбінації носіїв:
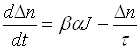 . (3.5)
. (3.5)
Другий член в
рівнянні (3.5) враховує зменшення концентрації неосновних носіїв заряду в
результаті процесу рекомбінації. Інтенсивність рекомбінації можна вважати
пропорційною концентрації нерівноважних носіїв тільки в тому випадку, якщо час
життя нерівноважних носіїв τ (однаковий для електронів і дірок) не
залежить від їх концентрації.
Ця умова
виконується, коли концентрація нерівноважних носіїв Δn, Δp мала у порівнянні з концентрацією рівноважних основних
носіїв заряду (наприклад, Δp=Δn<<p0), так як при зміні концентрації
основних носіїв під дією освітлення можна знехтувати і вважати її постійною.
Цей випадок має місце, наприклад, у домішковому напівпровіднику при генерації
фотоносіїв в області фундаментального поглинання при такій температурі, коли
вся домішка іонізована.
Знайдемо
розв’язок (3.5), вважаючи, що Δp=Δn<<p0 і p0<<n0 і що напівпровідник починає
освітлюватись в момент t=0 світлом постійної інтенсивності. Тоді, розділюючи змінні і інтегруючи
з врахуванням початкової умови Δn=0 при t=0, одержуємо
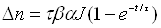 . (3.6)
. (3.6)
Усталене значення
нерівноважної концентрації електронів Δn0 визначається з (3.6) при 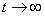 :
:
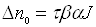 . (3.7)
. (3.7)
Якщо, навпаки, в зразку створена стаціонарна концентрація нерівноважних
носіїв Δn0 і в
момент t=0 світло
вимикається, то концентрація нерівноважних носії заряду спадає до нульового
значення по закону
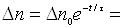
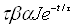 . (3.8)
. (3.8)
Таким чином, релаксація (тобто наростання або спадання) нерівноважних
концентрацій носіїв заряду при миттєвому ввімкненні і вимкненні світла
відбувається по експоненціальному закону з постійною часу τ, яка
відповідає часу життя нерівноважних носіїв заряду.
Одержані аналітичні залежності для наростання концентрації
нерівноважних носіїв заряду дають можливість визначити закон зміни
нерівноважної стаціонарної фотопровідності (концентрації) від інтенсивності
освітлення, тобто люксамперні характеристики. При лінійному законі
рекомбінації, коли час життя нерівноважних носіїв заряду не залежить від
інтенсивності освітлення, люксамперна характеристика лінійна, так як у
відповідності з (3.7) стаціонарна нерівноважна концентрація Δn0 пропорційна
інтенсивності світла J.
Принципова схема вимірювальної для дослідження фотопровідності
приведена на рис. 3.2.
Світло від джерела світла EL1 з допомогою оптичної системи ОС фокусується на вхідну щілину S1 монохроматора СФ–4. Світловий потік можна
послаблювати з допомогою нейтрально сірих фільтрів НСФ. З вихідної щілини S2 монохроматора випромінювання направляється
на зразок напівпровідника R і
повністю поглинаючись в ньому, створюює фотопровідність. Зміна опору зразка
приводить до зміни струму в колі, який фіксується мікроамперметром РА1.
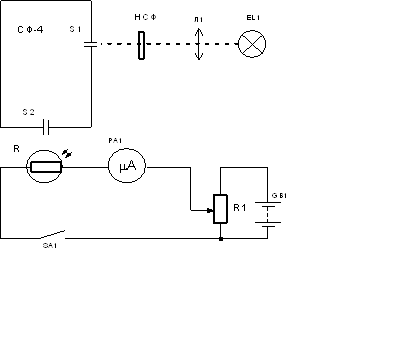
Рис. 3.2 Принципова схема вимірювальної установки
Джерелом світла у вимірювальній установці є вольфрамова лампа
розжарювання. Колірна температура нитки розжарювання 1800 К.
Дисперсія світла по довжинах хвиль здійснюється з допомогою
спектрофотометра СФ–4. Величина спектрального інтервалу δλ, який
виходить з спектрального приладу, залежить від ширини вихідної щілини S2 і дисперсії приладу D(λ): δλ=S2D(λ).
Кількість світлової енергії, яка проходить через вихідну щілину
монохроматора,
δE(λ)=aρ(λ)δλ=aρ(λ)S2D(λ), (3.9)
де a – коефіцієнт
пропорціональності, 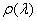 – спектральна густина
випромінювання.
– спектральна густина
випромінювання.
Крива дисперсії задається в додатку до вимірювальної установки.
Завдання до лабораторної роботи
1. Ознайомитися з приладами, які
використовуються в лабораторній роботі. При необхідності провести юстування
оптичної системи установки.
2. Виміряти спектральну залежність величини
фотоструму, проводячи вимірювання через 50–100 Ǻ. Результати вимірювань
занести в таблицю.
Послідуючий аналіз результатів зручно проводити
представивши спектральну залежність фотопровідності у відносних одиницях. Для
цього потрібно провести нормування фотоструму до одиниці
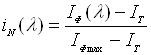 ,
,
де ІФ(λ) – фотострум при
заданій довжині хвилі, ІТ – темновий струм (при відсутності
освітлення), ІФ max – максимальне значення фотоструму в умовах досліду.
Провести перерахунок одержаних результатів на
одиницю падаючої енергії і на однакову кількість падаючих фотонів, тобто обчислити
величини
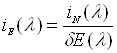 та
та 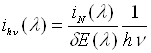 ,
,
де δE(λ) знаходиться з виразу (3.9). Результати
обчислень занести в таблицю.
3. Побудувати всі три криві у довільному
масштабі на одному графіку.
4. Визначити
ширину забороненої зони Eg досліджуваного напівпро-відникового матеріалу, скориставшись
для цього спектральним положенням максимуму фотопровідності.
5. Провести
вимірювання люксамперних характеристик зразка в області максимуму
фотопровідності, змінюючи інтенсивність освітлення з допомогою світлофільтрів.
6. Побудувати люксамперну характеристику
у відносних одиницях.
7. Проаналізувати
одержані результати та зробити висновки.
Література
[1]. c. 211-236. [2]. c. 221-245. [4]. с. 221–266, 383–395.
ЛАБОРАТОРНА РОБОТА №4
Дослідження
впливу електричного поля на електропровідність напівпровідників
Мета роботи:
експериментальна перевірка впливу електричного поля на електропровідність
напівпровідників та встановлення механізму впливу.
Необхідні прилади
і матеріали: регульоване джерело постійної напруги; мікроамперметр; вольтметр;
термостат з системою регулювання та контролю температури.
Теоретичні питання знання, яких
необхідне для виконання лабораторної роботи:
1. Генерація нерівноважних носіїв заряду під
дією сильного електричного поля.
2. Вплив електричного поля на рухливість носіїв заряду. “Розігрів”
електронного газу.
3. Міждолинне розсіювання. Ефект Ганна.
Основні теоретичні відомості та
методика експерименту
Якщо концентрації електронів n та дірок р і, відповідно їх рухливості 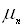 ,
, 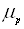 не залежать від напруженості
електричного поля
не залежать від напруженості
електричного поля  , то залежність густини струму
, то залежність густини струму 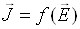 описується
законом Ома у диференціальній формі:
описується
законом Ома у диференціальній формі:
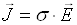 , де
, де
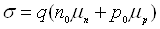 . (4.1)
. (4.1)
У випадку, коли 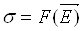 , залежність
(4.1) не виконується. Це може бути пов’язано з тим, що при великих
напруженостях електричного поля може відбуватись зміна концентрації носіїв
заряду (польова генерація) та рухливості носіїв заряду.
, залежність
(4.1) не виконується. Це може бути пов’язано з тим, що при великих
напруженостях електричного поля може відбуватись зміна концентрації носіїв
заряду (польова генерація) та рухливості носіїв заряду.
При збільшенні напруженості електричного поля дрейфова швидкість носіїв
заряду 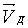 зростає
і може виявитись, що вона стає порівняною з середньою тепловою швидкістю
зростає
і може виявитись, що вона стає порівняною з середньою тепловою швидкістю 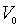 . У цьому
випадку рухливість носіїв заряду починає залежати від Е і закон Ома
порушується. Поля, при яких проявляється така залежність, називаються сильними.
Гранична напруженість ЕК, з якої проявляється помітне відхилення від
закону Ома, називається критичною.
. У цьому
випадку рухливість носіїв заряду починає залежати від Е і закон Ома
порушується. Поля, при яких проявляється така залежність, називаються сильними.
Гранична напруженість ЕК, з якої проявляється помітне відхилення від
закону Ома, називається критичною.
Збільшення швидкості електронів під дією зовнішнього поля можна
трактувати як ефект “збільшення” температури у порівнянні з температурою
кристалічної гратки – ефект розігріву електронів. Такі електрони мають енергію,
більшу рівноважної теплової енергії, яка відповідає температурі гратки. Їх
називають “гарячими” електронами.
Характер розігріву електронів може мати різний характер. В полях з
відносно невеликою напруженістю електрони набувають незначну енергію. Але якщо
ця енергія виявляється більшою за ту, яку вони втрачають при зіткненнях, то їх
швидкість буде поступово зростати і електронний газ буде поступово
розігріватись. Так як приріст швидкості направленого руху на довжині вільного
пробігу електронами швидко втрачається в наступних зіткненнях, то розігрів
електронного газу в цьому випадку зумовлений в основному ростом швидкості
хаотичного руху.
В полях високої напруженості, навпаки, розігрів електронного газу
відбувається в основному внаслідок направленої складової швидкості руху
електронів. З збільшенням 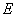 ця складова швидкості руху, а
разом з нею і температура електронного газу можуть зростати, очевидно, до тих
пір, поки енергія накопичена електронами на довжині вільного пробігу, не
виявиться достатньою для збудження оптичних фононів. Зіткнення електронів з
граткою стають у цьому випадку непружними і супроводжуються втратою накопиченої
ними енергії і появою оптичних фононів.
ця складова швидкості руху, а
разом з нею і температура електронного газу можуть зростати, очевидно, до тих
пір, поки енергія накопичена електронами на довжині вільного пробігу, не
виявиться достатньою для збудження оптичних фононів. Зіткнення електронів з
граткою стають у цьому випадку непружними і супроводжуються втратою накопиченої
ними енергії і появою оптичних фононів.
Як показує розрахунок при розсіюванні на акустичних фононах в сильних
електричних полях рухливість обернено пропорційна кореню квадратному з
напруженості електричного поля:
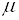 ~
~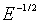 . (4.2)
. (4.2)
Але для випадку розсіювання на оптичних коливаннях іонної гратки при
температурі нижче дебаївської одержують
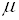 ~
~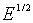 . (4.3)
. (4.3)
У більшості випадків мають справу з залежністю (4.2), де з ростом
напруженості електричного поля рухливість зменшується.
Зміна концентрації носіїв заряду в сильних електричних полях може
відбуватись в результаті дії ряду механізмів. Одним з таких механізмів є
термоелектронна іонізація Френкеля.
Електричне поле  , створене в напівпровіднику,
змінює енергетичний стан електронів в атомі. На рис. 4.1 пунктиром показана
потенціальна яма донорного атома в напівпровіднику при відсутності електричного
поля. Яма симетрична відносно осі енергій. Під дією зовнішнього поля
, створене в напівпровіднику,
змінює енергетичний стан електронів в атомі. На рис. 4.1 пунктиром показана
потенціальна яма донорного атома в напівпровіднику при відсутності електричного
поля. Яма симетрична відносно осі енергій. Під дією зовнішнього поля  яма
деформується так як показано на рис. 4.1 суцільною лінією. Енергія активації,
необхідна, для теплового викиду електрона з домішкового рівня
яма
деформується так як показано на рис. 4.1 суцільною лінією. Енергія активації,
необхідна, для теплового викиду електрона з домішкового рівня 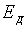 в зону провідності, зменшується на
в зону провідності, зменшується на 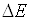 .
.
Як показує розрахунок, це зменшення пропорційне  , внаслідок чого
ймовірність теплового збудження електронів у провідний стан зростає в
, внаслідок чого
ймовірність теплового збудження електронів у провідний стан зростає в 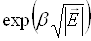 (
(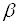 – коефіцієнт
пропорціональності), що викликає збільшення в
– коефіцієнт
пропорціональності), що викликає збільшення в 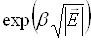 концентрації носіїв заряду і
електропровідності напівпровідників:
концентрації носіїв заряду і
електропровідності напівпровідників:
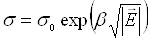 .
(4.4)
.
(4.4)
Співвідношення (4.4) називається законом Френкеля.
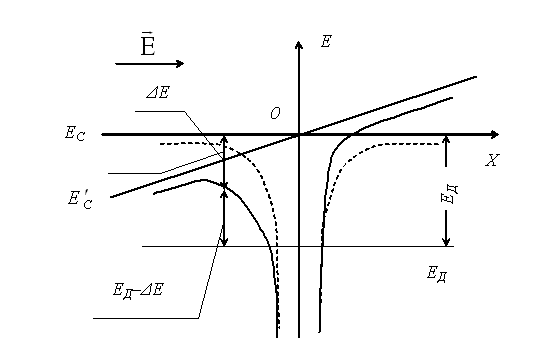
Рис. 4.1 Деформація потенціальної ями домішкового атома під дією
зовнішнього електричного поля, яка приводить до зменшення енергії активації
домішкової електропровідності (ефект Френкеля)
Для більш слабких полів теорія приводить до закону Пуля:
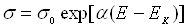 ,
(4.5)
,
(4.5)
де 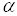 –
залежний від температури коефіцієнт.
–
залежний від температури коефіцієнт.
Під впливом зовнішнього електричного поля енергетичні зони
напівпровідника нахиляються так, як показано на рис. 4.2,а. Це створює умови
для двоякого переходу в зону провідності: по вертикалі 1 і по горизонталі 2.
Перехід 1 потребує затрати енергії і здійснюється шляхом теплового
збудження або ударної іонізації.
Ударна іонізація відбувається в полях, здатних вільному електрону зону
провідності надати енергію, достатню для того, щоб при зіткненні з атомами він
був в стані достатньому для їх іонізації. Якщо при цьому іонізуючий електрон
залишається в зоні провідності, то число вільних електронів буде неперервно
збільшуватись.
Залежно від величини напруженості електричного поля ударна іонізація
протікає по різному. В полях низької напруженості електрон на довжині вільного
пробігу набуває тільки незначну частку енергії, необхідної для іонізації атома.
Але якщо при зіткненнях з атомами електрон втрачає частку енергії меншу, чим
набуває на довжині вільного пробігу, то швидкість його буде неперервно зростати
і в кінцевому результаті стає достатньою для іонізації атома. Цей випадок
показано на рис. 4.2,б. Таку ударну іонізацію називають низьковольтною.
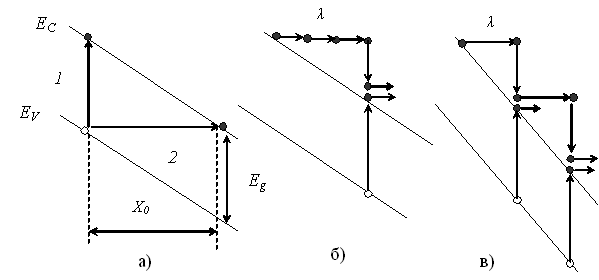
Рис. 4.2 Іонізація напівпровідника під дією сильного електричного поля:
а – способи переходу електрона в зону провідності під дією сильного
електричного поля: 1 – шляхом ударної іонізації; 2 – шляхом тунельного
просочування; б – розігрів електронів зони провідності в полях відносно
невисокої напруженості, який приводить до ударної іонізації; в – ударна
іонізація в сильних електричних полях
В полях високої напруженості електрон може набувати енергію, необхідну
для іонізації атома, вже на одній довжині вільного пробігу (рис. 4.2в). таку
ударну іонізацію називають високовольтною.
Горизонтальні переходи 2 відбуваються без затрати енергії шляхом
тунельного просочування електронів через заборонену зону. Цей механізм
називають електростатичною іонізацією або ефектом Зінера. Ймовірність його w сильно залежить від ширини забороненої зони і
напруженості електричного поля. Фактично цей перехід відбувається через
трикутний потенціальний бар’єр висотою Eg та шириною X0.
Для переходів типу 2 розрахунок приводить до наступного виразу
для w:
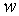 ~
~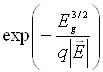 .
(4.6)
.
(4.6)
Оцінка по цій формулі показує, що при 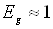 еВ ймовірність w стає помітною при
еВ ймовірність w стає помітною при 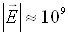 В/м. У
домішкових напівпровідниках помітна електростатична іонізація спостерігається
уже в полях з напруженістю
В/м. У
домішкових напівпровідниках помітна електростатична іонізація спостерігається
уже в полях з напруженістю 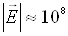 В/м. З (4.6) слідує, що w, відповідно і концентрація носіїв заряду,
генерованих в напівпровіднику під дією електричного поля
В/м. З (4.6) слідує, що w, відповідно і концентрація носіїв заряду,
генерованих в напівпровіднику під дією електричного поля  , не залежить від
температури.
, не залежить від
температури.
(для випадку коли ширина забороненої зони не залежить від температури).
Для більшості напівпровідників Eg з збільшенням температури
зменшується і, відповідно, це приводить до зростання ймовірності тунельних
переходів і зростання струму. Тобто при електростатичній іонізації
температурний коефіцієнт спаду напруги є від’ємним на відміну від
термоелектронної і ударної іонізації.
Збільшення концентрації носіїв заряду в результаті ударної і
електростатичної іонізації не носить на перших порах лавинного характеру, так
як вріноважується процесом рекомбінації, який протікає з тим більшою швидкістю,
чим більше утворюється електронів в зоні провідності і дірок у валентній зоні.
Але в дуже сильних електричних полях (порядку 107–109
В/м) починається лавинний характер наростання числа носіїв, який
супроводжується пробоєм напівпровідника.
На рис. 4.3 приведена якісна крива зміни питомої електропровідності
напівпровідника з підвищенням напруженості електричного поля 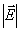 і вказані (орієнтовно)
критичні значення напруженостей переходу від одного механізму зміни σ до
іншого.
і вказані (орієнтовно)
критичні значення напруженостей переходу від одного механізму зміни σ до
іншого.
Експериментально встановити вплив електричного поля на
електропровідність напівпровідників можна шляхом дослідження вольт-амперних
характеристик (ВАХ). Температурні дослідження дають можливість встановити
механізм польової генерації. Принципова електрична схема для дослідження ВАХ
представлена на рис. 4.4.
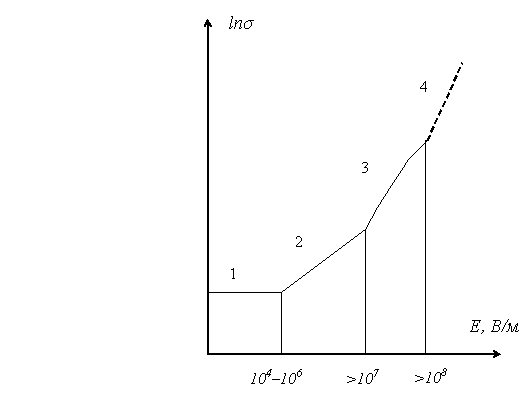
Рис. 4.3 Якісна залежність зміни питомої електропровідності
напівпровідника від напруженості електричного поля: 1 – ділянка Ома; 2 –
ділянка Френкеля або Пуля; 3 – ділянка електростатичної іонізації; 4 – пробій
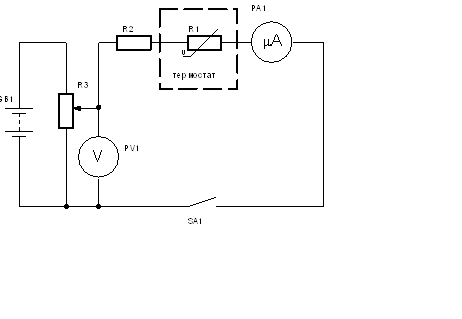
Рис. 4.4 Принципова електрична схема для дослідження ВАХ
При температурних дослідженнях зразок поміщають у термостат. За
експериментально виміряними характеристиками будують графіки I=f(U). З цих залежностей визначають:
– статичний опір
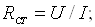 (4.7)
(4.7)
– динамічний опір
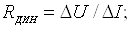 (4.8)
(4.8)
– коефіцієнт нелінійності k, який показує, у скільки разів 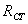 при заданій
напрузі більший
при заданій
напрузі більший 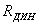 ,
,
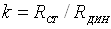 ;
(4.9)
;
(4.9)
– температурний коефіцієнт зміни струму
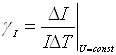 ;
(4.10)
;
(4.10)
– температурний коефіцієнт зміни спаду напруги
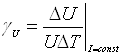 .
(4.11)
.
(4.11)
Завдання до лабораторної роботи
1. Зібрати електричну схему, зображену на рис. 4.4. виміряти статичну
ВАХ при температурах 300, 330, 360 К.
2. Обчислити електропровідність σ матеріалу при різних напругах
для T=const.
3. Побудувати графіки залежності lnσ=f(E) або lnσ=f(U) для вимірюваних температур.
4. За формулами (4.7) – (4.11) основні параметри досліджуваного зразка.
Проаналізувати механізм впливу температури на ВАХ та визначити механізм польової
генерації.
5. Обчислити похибки вимірювань та зробити висновки.
Література
[1]. c. 320-331. [2]. c. 348-363. [4]. с. 288-301. [5]. с.
191-210.
ЛАБОРАТОРНА
РОБОТА №5
Експериментальне
вивчення ємнісних властивостей електронно-діркових переходів
Мета роботи:
дослідження вольт-фарадних характеристик (ВФХ) p-n переходів та визначення
параметрів напівпровідникового матеріалу.
Необхідні прилади
і матеріали: регульоване джерело постійної напруги; вольтметр; прилад для
вимірювання електричної ємності; досліджувані зразки.
Теоретичні питання знання, яких
необхідне для виконання лабораторної роботи:
1. Глибина екранування зовнішнього електричного
поля.
2. Товщина p-n переходу та її залежність від напруги, концентрації та
характеру розподілу легуючих домішок.
3. Дифузійна та бар’єрна ємності p-n переходу.
Основні теоретичні відомості та
методика експерименту
Інжекція неосновних носіїв заряду (при прикладанні до p-n переходу
прямої напруги) і екстракція неосновних носії (у випадку зворотної напруги),
приводять до зміни, порівняно з рівноважними концентраціями, сумарного
об’ємного заряду у електронейтральних областях p-n переходу.
Зміну сумарного заряду об’ємного Q, для прямо зміщеного p-n переходу,
можна розглядати як дію деякої ємності С. Ця ємність одержала назву дифузійної
(СДИФ). СДИФ можна знайти, виходячи з відомої залежності 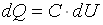 і, у випадку
емітера р-типу, її залежність від струму p-n переходу задається виразом:
і, у випадку
емітера р-типу, її залежність від струму p-n переходу задається виразом:
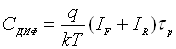 ,
(5.1)
,
(5.1)
де IF і IR – значення прямого і зворотного
струмів відповідно, τр – час життя дірок, q – заряд електрона.
Це рівняння показує, що дифузійна ємність проявляється при прямих
напругах і збільшується з ростом прямого струму. При зворотних напругах вклад
цієї ємності є незначним в силу значно меншої величини зворотного струму і при
досягненні цим струмом постійного значення є сталою величиною.
Таким чином, СДИФ при великих зворотних напругах не
проявляється. Але у цьому випадку суттєвим є прояв так званої зарядової або
бар’єрної ємності. Формування і зміна цієї ємності полягає у наступному.
При прикладанні до p-n переходу зворотної напруги основні і неосновні
носії вільні заряду виштовхуються (екстрагуються з прилягаючих до границь
розділу шарів різного типу електропровідності). В результаті залишаються
некомпенсовані об’ємні заряди нерухомих донорів і акцепторів. Очевидно, що чим
з більшого об’єму будуть виштовхнуті полем рухомі носії заряду, тобто чим
більші товщини dn і dp
шарів об’ємного заряду, тим більша величина об’ємних некомпенсованих зарядів.
Ця зміна об’ємних зарядів у p-n переході при зміні зворотної напруги і визначає
роботу p-n переходу як електрично керованої ємності. Її вплив в електричних
схемах проявляється в тому випадку, коли напруга на p-n переході змінюється з
часом. Тоді окрім струму, який визначається статичною ВАХ, протікає додатковий
ємнісний струм, рівний C(dU/dt). Він зв’язаний з зміною об’ємних зарядів з часом: I(t)=dQ/dt=(dQ/dU)* *(dU/dt). Тому бар’єрна ємність C=Cбар=dQ/dU. На відміну від звичайного конденсатора відношення заряду до повної
напруги на p-n переході 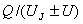 не рівне його ємності, так як
не рівне його ємності, так як 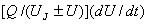 не дає
ємнісного струму. Це пояснюється нелінійністю залежності Q(U); по цій же причині
бар’єрна ємність залежить від напруги.
не дає
ємнісного струму. Це пояснюється нелінійністю залежності Q(U); по цій же причині
бар’єрна ємність залежить від напруги.
У випадку несиметричного p+-n переходу (Na>>Nd) з ступінчатим розподілом домішки об’ємний заряд
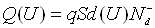 ,
(5.2)
,
(5.2)
де 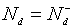 –
концентрація донорів в базі,
–
концентрація донорів в базі, 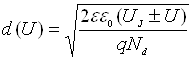 – товщина збідненого шару
несиметричного p-n переходу, UJ – контактна різниця потенціалів.
– товщина збідненого шару
несиметричного p-n переходу, UJ – контактна різниця потенціалів.
Тоді, враховуючи вище викладене одержуємо вираз для бар’єрної
(зарядової) ємності
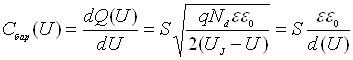 .
(5.3)
.
(5.3)
Останній запис формули (5.3) справедливий для p-n переходу з будь-яким
розподілом концентрацій домішок. З неї видно, що зарядова ємність співпадає з
ємністю плоского конденсатора з віддалю між обкладками, рівній товщині
збідненого шару. Аналогія з плоским конденсатором дозволяє наглядно пояснити
властивості бар’єрної ємності. Наприклад, з ростом модуля зворотної напруги
зарядова ємність зменшується, що зумовлено зростанням товщини p-n переходу,
тобто віддалі між обкладками конденсатора. Збільшення концентрації легуючих
домішок збільшує ємність, так як віддаль між обкладками зменшується.
Для плавного p-n переходу з лінійним розподілом домішок бар’єрна
ємність визначається наступним виразом:
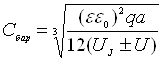 ,
(5.4)
,
(5.4)
де а – градієнт концентрації.
Залежність ємності від напруги називається вольт-фарадною
характеристикою. По ВФХ можна визначити тип переходу.
Схема, яка використовується для вимірювання ВФХ у цій лабораторній
роботі, приведена на рис. 5.1. Конденсатор С1 запобігає попаданню постійної
складової напруги на вхід приладу для вимірювання ємності. Якщо С1>>Cбар то його
ємність не враховується. Резистор R2 зменшує шунтуючу дію вхідного вольтметра V (R2=100 кОм).
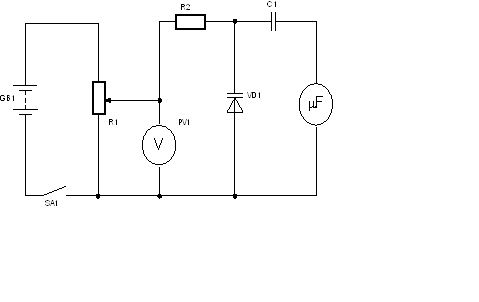
Рис. 5.1 Схема для дослідження вольт-фарадних характеристик p-n
переходу
Завдання до лабораторної роботи
1. Дослідити залежність бар’єрної (зарядової) ємності Cбар від величини
зворотної напруги U прикладеної до діода
[вольт-фарадну характеристику C=f(U)].
2. Побудувати графіки залежностей (1/С)2=f(U) і (1/С)3=f(U).
По одержаних графіках визначити:
а) тип переходу (різкий або плавний);
б) для різкого p-n переходу екстраполюючи графік залежності (1/С)2=f(U)
до значення (1/С)2=0 визначити контактну різницю потенціалів UJ;
в) концентрацію донорів Nd. Для цього використати формулу (5.3) і залежність (1/С)2=f(U).
При розрахунках прийняти, що S=0,5
мм2, ε=11,6 (Si).
3. По виміряних значеннях С за формулою для ємності плоского
конденсатора розрахувати і побудувати графік залежності товщини p-n переходу d від зовнішньої напруги U.
4. Знайти положення рівня Фермі, допустивши, що донорна домішка при
температурі досліду є повністю іонізована, тобто рівноважна концентрація
вільних носіїв 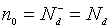 . Для визначення використайте
формулу, яка встановлює зв’язок між положенням рівня Фермі і концентрацією рівноважних
носіїв заряду
. Для визначення використайте
формулу, яка встановлює зв’язок між положенням рівня Фермі і концентрацією рівноважних
носіїв заряду
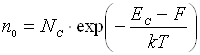 . (5.5)
. (5.5)
Згідно закону діючих мас  , визначити концентрацію
неосновних носіїв заряду – дірок. Матеріал – кремній.
, визначити концентрацію
неосновних носіїв заряду – дірок. Матеріал – кремній.
5. На основі одержаних результатів побудувати енергетичну діаграму p-n
переходу в рівноважному стані. Прийняти Eg=1,1 еВ.
6. Обчислити похибки вимірювань. Проаналізувати одержані результати та
зробити висновки.
Література
[1]. c. 320-331. [2]. c. 348-363. [4]. с. 221-266, 288-301. [5]. с. 135-170, 191-210.
ЛАБОРАТОРНА РОБОТА №6
Дослідження
впливу температури на вольт-амперну характеристику p-n переходу
Мета роботи: експериментально
встановити залежність властивостей p-n переходу від температури та визначити
контактну різницю потенціалів, опір бази та складові зворотного струму.
Необхідні прилади
і матеріали: регульоване джерело постійної напруги; вольтметр (0-300 В);
мілівольтметр (0-1000 мВ); мілі- та мікроамперметр; термостат з системою
стабілізації та контролю температури; германієві та кремнієві площинні діоди.
Теоретичні питання знання, яких
необхідне для виконання лабораторної роботи:
1. Фізичні процеси, які відбуваються в результаті
контакту напівпровідників з різним типом провідності.
2. Електронно-дірковий перехід у рівноважному стані. Енергетична
діаграма.
3. Інжекція та екстракція носіїв заряду.
4. Вольт амперна
характеристика (ВАХ) p-n переходу. Генерація та рекомбінація в області
просторового заряду (ОПЗ). Вплив температури на ВАХ.
5. Випрямлення на
p-n переході.
6.
Гетеропереходи.
Основні теоретичні відомості та
методика експерименту
Рівняння залежності густини струму через ідеальний p-n перехід від
прикладеної напруги має вигляд:
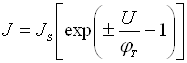 ,
(6.1)
,
(6.1)
де U – спад напруги на p-n
переході (знак “+” відповідає прямому зміщенню переходу , “–“ – зворотному), JS – густина струму термічної генерації
(тепловий струм або струм насичення), 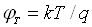 – температурний потенціал (при
Т=300 К φТ=0,026 еВ). Для симетричного тонкого p-n переходу
густина теплового струму
– температурний потенціал (при
Т=300 К φТ=0,026 еВ). Для симетричного тонкого p-n переходу
густина теплового струму
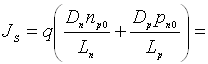
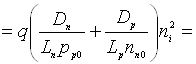
 , (6.2)
, (6.2)
де Dn(p) – коефіцієнт
дифузії електронів (дірок); Ln(p) – дифузійна довжина електронів (дірок); τn(p) – час життя електронів (дірок); ni – концентрація носіїв заряду у
власному напівпровіднику.
Для несиметричного p+-n переходу у якому Na>>Nd і, відповідно, pp0>>nn0 густина теплового
струму 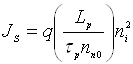 . Якщо густину струму помножити на
площу переходу S, то одержимо
значення теплового струму
. Якщо густину струму помножити на
площу переходу S, то одержимо
значення теплового струму
 (6.3)
(6.3)
З останнього слідує фізичний зміст теплового струму – IS можна представити як струм, що
виникає в результаті теплової генерації дірок в квазінейтральній n-базі в об’ємі SLp з швидкістю pn0/τp (дірок в см3 за
секунду), тобто в шарі бази товщиною Lp,
яка прилягає до границі ОПЗ.
Як слідує з (6.1) при зворотній напрузі UR>3φT, експоненціальна складова
стає значно меншою за одиницю і її можна не враховувати. Зворотний
струм через перехід визначають значенням теплового струму, який, відповідно до
(6.2) та (6.3), є постійною величиною не залежною від напруги:
IR=–IS=const. (6.4)
Експериментально встановлено, що вираз (6.1) задовільно описує ВАХ p-n
переходів виготовлених на основі напівпровідників з малою шириною забороненої
зони, включаючи германій (Eg=0,66 еВ). Зворотні ділянки ВАХ кремнієвих, арсенідогалієвих,
фосфідогалієвих p-n переходів не мають ділянки насичення. Для пояснення цього
необхідно врахувати теплову генерацію в ОПЗ p-n переходу.
При зворотній напрузі на p-n переході область ОПЗ збіднена носіями
заряду і рівновага між процесами генерації і рекомбінації порушена в бік
генерації носіїв заряду. Це в основному обумовлено наявністю локальних рівнів
поблизу середини Eg.
У результаті генерації пар електрон-дірка виникає зворотний струм IRG,
який пропорційний об’єму ОПЗ S·d(U) і швидкості генерації у збідненому шарі G=ni/(2τ0),
де – τ0=τn=τp час життя носіїв
заряду в ОПЗ. По аналогії з (6.3) можемо записати:
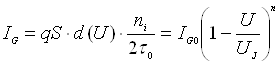 ,
(6.5)
,
(6.5)
де – 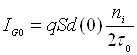 ; n=1/2 для різкого і n=1/3 для
плавного p-n переходів; UJ
; n=1/2 для різкого і n=1/3 для
плавного p-n переходів; UJ
– контактна різниця потенціалів.
Струм генерації зростає при збільшенні зворотної напруги, що пов’язано
з розширенням збідненого шару. З (6.3) і (6.5) слідує
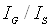 ~
~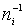 ~
~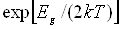 ,
,
тобто вклад струму генерації в повний зворотний струм тим більший, чим
більша ширина забороненої зони і нижча температура. Наприклад, для кремнієвого
p-n переходу при Т=25°С і U=–1 B одержуємо IG=10-9
A, a I0=10–14 A.
Реальні p-n переходи мають ділянки, які виходять на поверхню ділянки
напівпровідникового кристалу. На поверхні внаслідок забруднень і впливу
поверхневого заряду між р– і n–областями
можуть утворюватись провідні плівки і канали, по яких протікає струм утрат. Він
зростає пропорційно напрузі і при достатньо великій напрузі може перевищити
тепловий струм і струм генерації. Для струму втрат характерна незначна
залежність від температури. В кремнієвих приладах поверхня кристала покрита
захисним шаром оксиду і цей струм, як правило, є, нехтуючи малим.
Враховуючи останнє можна записати, що зворотний струм реального p-n
переходу визначається, в основному, як сума теплового струму та струму
генерації:
IR=–IS –ІG. (6.6)
З всіх електрофізичних параметрів, які входять у вирази для 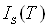 та
та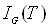 , найбільшу
залежність від температури має власна концентрація носіїв заряду ni:
, найбільшу
залежність від температури має власна концентрація носіїв заряду ni:
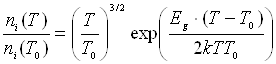 .
(6.7)
.
(6.7)
Нехтуючи степеневими залежностями від температури порівняно з
експоненціальною, одержуємо:
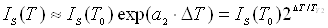 ;
(6.8)
;
(6.8)
 ,
(6.9)
,
(6.9)
де 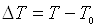 ;
;
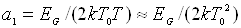 ;
; 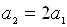 ;
;  ;
;
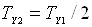 ;
; 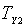 ,
, 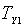 – температури подвоєння відповідного струму.
– температури подвоєння відповідного струму.
Для кремнію температура подвоєння струму 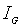 складає
складає 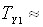 9°С, а для
9°С, а для 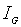 значення
значення 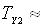 4 К, поблизу 300 К. Для германієвих p-n переходів за
звичай
4 К, поблизу 300 К. Для германієвих p-n переходів за
звичай 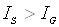 , а
для кремнієвих
, а
для кремнієвих  при Т=300 К, але при максимально
допустимих температурах кремнієвих p-n переходів, що досягають 150–170°С, струм
насичення може перевищувати струм генерації за рахунок більш сильного зростання
струму насичення з температурою.
при Т=300 К, але при максимально
допустимих температурах кремнієвих p-n переходів, що досягають 150–170°С, струм
насичення може перевищувати струм генерації за рахунок більш сильного зростання
струму насичення з температурою.
При прямій напрузі на p-n переході в результаті зниження висоти
потенціального бар’єру концентрація носіїв заряду в ОПЗ переходу зростає і стає
більшою за рівноважну. Тому в ОПЗ може відбуватись рекомбінація електронів і
дірок. Струм рекомбінації в ОПЗ p-n переходу
 ,
(6.10)
,
(6.10)
де 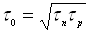 –
час життя носіїв заряду в ОПЗ переходу.
–
час життя носіїв заряду в ОПЗ переходу.
Передекспоненціальний множник залежить від напруги через залежність
товщини ОПЗ від напруги і наявність множника 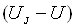 в знаменнику. Але ця залежність
значно слабша за експоненціальну, і в першому наближенні можна вважати, що
струм
в знаменнику. Але ця залежність
значно слабша за експоненціальну, і в першому наближенні можна вважати, що
струм 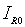 має
постійне значення.
має
постійне значення.
В широкозонних напівпровідниках при малих прямих напругах ( ) струм
рекомбінації в ОПЗ може виявитись більшим за струм інжекції, розрахований по
формулі (6.1). але з ростом прямої напруги через наявність в знаменнику
показника експоненти множника 2 струм IRG зростає значно повільніше, чим струм інжекції, і в робочому діапазоні
струмів переважає струм інжекції.
) струм
рекомбінації в ОПЗ може виявитись більшим за струм інжекції, розрахований по
формулі (6.1). але з ростом прямої напруги через наявність в знаменнику
показника експоненти множника 2 струм IRG зростає значно повільніше, чим струм інжекції, і в робочому діапазоні
струмів переважає струм інжекції.
Повний струм через p-n перехід при прямій напрузі рівний сумі струмів
інжекції і рекомбінації носіїв заряду в ОПЗ:
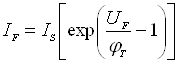
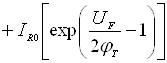 . (6.11)
. (6.11)
Слід зауважити, що з ростом температури співвідношення струмів інжекції
і рекомбінації в ОПЗ змінюється: струм IR0 зростає значно слабше,
так як він ~ni, а струм інжекції IS ~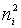 .
.
Збільшення температури приводить до зменшення контактної різниці
потенціалів
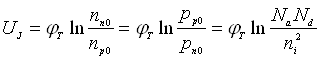 (6.12)
(6.12)
і, відповідно, до зменшення висоти потенціального бар’єру і зменшення
прямого спаду напруги при постійному значенні струму. Температурний коефіцієнт
прямого спаду напруги (ТКUF) є від’ємним і складає –(1,5÷3,5) мВ/К. При розрахунках приймають ТКUF=
–2 мВ/К.
Для дослідження прямої ділянки ВАХ p-n переходу використовується
принципова електрична схема приведена на рис. 6.1а). Спад напруги на діоді
визначають мілівольтметром mV,
який безпосередньо приєднаний до діода VD1, а струм у колі вимірюють міліамперметром mA. У випадку зворотного включення (рис. 6.1б) струм у колі вимірюють
мікроамперметром μА, а напруга вимірюється вольтметром V, який ввімкнено на вихід регульованого
джерела напруги для усунення шунтування діода вольтметром.
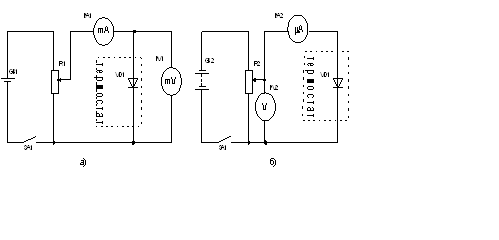
Рис. 6.1 Принципова електрична схема для дослідження ВАХ p-n переходу
Завдання до лабораторної роботи
1. Зібрати схеми зображені на рис. 6.1 а, б і дослідити прямі та
зворотні ділянки ВАХ кремнієвого діода. При 295, 305, 315, 325, 335, 350 та 370
К.
2. Побудувати ВАХ на одному графіку та визначити при однакових
температурах такі величини:
а) статичний опір для прямого та зворотного зміщень RCT=U/I та диференціальний опір rдиф=ΔU/ΔI;
б) коефіцієнт випрямлення k=Iпр/Iзв при Uпр=Uзв.
3. Для Uпр>0,7 В визначити опір бази діода RБ=ΔU/ΔI. Шляхом екстраполяції цієї ділянки до Iпр=0
визначити контактну різницю потенціалів UJ.
4. Використовуючи результати температурних досліджень визначте
температурний коефіцієнт прямого спаду напруги ТКUF та температуру подвоєння зворотного струму.
5. Побудуйте залежність lnIзв=f(103/T) та за її
кутовим коефіцієнтом визначте ширину забороненої зони матеріалу діода.
6. Побудуйте енергетичну діаграму p-n переходу у рівноважному стані.
7. Проведіть обчислення похибок, зробіть найбільш важливі висновки.
Література
[1]. c. 320-331. [2]. c. 348-363. [4]. с. 288-301. [5]. с.
191-210.
ЛАБОРАТОРНА РОБОТА №7
Дослідження
механізмів пробою p-n переходу
Мета роботи: експериментальне
вивчення пробою p-n переходу та встановлення його механізму від температури та
визначення параметрів напівпровідникового матеріалу.
Необхідні прилади
і матеріали: регульоване джерело постійної напруги; вольтметр (0-300 В); мілі-
та мікроамперметр; термостат з системою стабілізації та контролю температури;
набір напівпровідникових стабілітронів.
Теоретичні питання знання, яких необхідне для виконання лабораторної
роботи:
1. Механізми пробою p-n переходів.
2. Вплив температури на напругу пробою.
3. Використання явищ пробою p-n переходів.
Основні теоретичні відомості та методика експерименту
Пробій p-n переходу – це явище різкого збільшення диференціальної
провідності p-n переходу у разі досягнення зворотною напругою (струмом)
критичного для даного приладу значення. Існують три основні види (механізми)
пробою: тунельний, лавинний і тепловий. Тунельний та лавинний відносять до електричних
пробоїв і вони є зворотними. Ці два типи пробою використовуються при
виготовлені напівпровідникових стабілітронів, тунельних діодів і т.д. Напругу,
при якій наступає пробій, називають напругою пробою Ub.
Тунельний пробій обумовлюється тунельним ефектом – переходом електронів
крізь потенціальний (енергетичний) бар’єр без зміни енергії. Тунельний ефект
виявляється тільки за дуже малої товщини переходу – порядку 10 нм, тобто в
переходах між сильнолегованими p+ і n+–областями (якщо Na, Nd>1018 см-3).
На рис. 7.1 показана енергетична діаграма p+-n+- переходу
при зворотній напрузі, стрілками позначено напрямок тунельного переходу
електрона з валентної зони р+-області в зону провідності n+-
області. Електрон тунелюючи з точки 1 в точку 2, проходить під енергетичним
бар’єром трикутної форми (заштрихований трикутник з вершинами в точках 1–3),
енергія електрона при цьому не змінюється.
Тунельні переходи можливі для електронів, енергія яких відповідає
інтервалу тунелювання ΔЕТ, в якому по обидві сторони
знаходяться дозволені рівні енергії. Висота бар’єру рівна ширині забороненої
зони Eg, вона, як
правило, менша висоти бар’єру p+-n+ -переходу, яка рівна q(UJ+|U|). Ширина бар’єра LT менша за товщину збідненого шару,
причому з ростом зворотної напруги ширина бар’єру зменшується, що збільшує
ймовірність тунелювання. Тунельний струм різко зростає, так як зростає інтервал
тунелювання і число електронів в ньому. Тунельний пробій в чистому вигляді
проявляється тільки при високих концентраціях домішки (більше 5·10 см-3),
а напруга пробою складає 0–5 В. при збільшенні температури ширина забороненої
зони дещо зменшується і напруга пробою знижується. Таким чином, температурний
коефіцієнт напруги тунельного пробою є від’ємним.
Тунельний пробій спостерігається при досягненні напруженістю електрич-
ного поля в ОПЗ певного критичного значення ЕК (для Ge EK=3·105
В/см, для Si EK=1,4·106 В/см). Зв’язок
цієї величини з напругою пробою Ub можна знайти прийнявши, що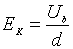 , де для тонкого
несиметричного переходу
, де для тонкого
несиметричного переходу 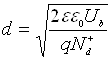 . Звідси одержуємо
. Звідси одержуємо
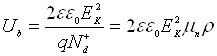 ,
(7.1)
,
(7.1)
де 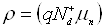 –
питомий опір слаболегованої області напівпровідника.
–
питомий опір слаболегованої області напівпровідника.
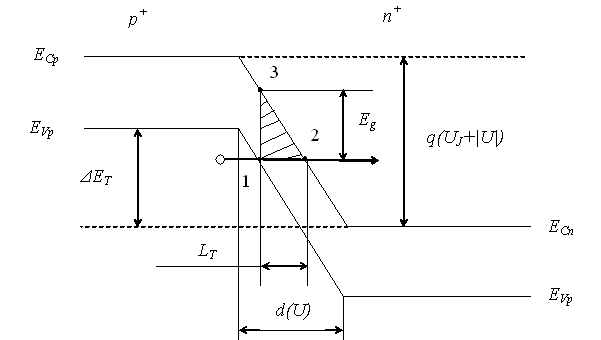
Рис. 7.1 Енергетична діаграма p-n переходу при тунельному пробої
Лавинний пробій пов’язаний з утворенням лавини носіїв заряду при дії
сильного електричного поля, в якій носії заряду на довжині вільного пробігу
набувають енергію достатню для утворення нових електронно-діркових пар шляхом
іонізації атомів напівпровідника. Для характеристики цього процесу
використовують коефіцієнт лавинного помноження М – рівний відношенню струму
носіїв заряду, що входять з однієї сторони збідненого шару до струму носіїв
того ж знаку які виходять з іншої сторони збідненого шару (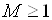 ). При збільшенні зворотної напруги значення М зростає. Для оцінки
використовують апроксимацію
). При збільшенні зворотної напруги значення М зростає. Для оцінки
використовують апроксимацію 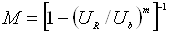 , де m – параметр, який і типу провідності залежить від матеріалу
напівпровідника p-n переходу. Для кремнію n-типу і германію р-типу m=5, для кремнію р-типу і германію n-типу m=3. Пробій зростає
при
, де m – параметр, який і типу провідності залежить від матеріалу
напівпровідника p-n переходу. Для кремнію n-типу і германію р-типу m=5, для кремнію р-типу і германію n-типу m=3. Пробій зростає
при 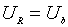 , що
відповідає
, що
відповідає 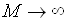 і
необмеженому зростанню струму. З врахуванням лавинного помноження ВАХ поблизу
напруги пробою може бути записаний у вигляді
і
необмеженому зростанню струму. З врахуванням лавинного помноження ВАХ поблизу
напруги пробою може бути записаний у вигляді 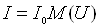 .
.
Чим більша ширина забороненої зони, тим більшу енергію має набрати
носій в електричному полі p-n переходу, щоб могла відбутись ударна іонізація.
При збільшенні температури напруга лавинного пробою зростає, що пов’язано з
зменшенням довжини вільного пробігу носіїв. При меншій довжині вільного пробігу
потрібна більша напруженість електричного поля для того, щоб носії набули
енергію, достатню для ударної іонізації.
Таким чином, температурний коефіцієнт напруги лавинного пробою
додатній.
Для практичних розрахунків використовується наступна емпірична
залежність напруги пробою від концентрації легуючої домішки та ширини забороненої
зони:
 ,
(7.2)
,
(7.2)
[Eg]=еВ, [N]=см–3.
При невеликих концентраціях домішок (менше 1018 см–3)
напруга лавинного пробою нижча, чим тунельного, тобто спостерігається лавинний
пробій. У цьому випадку 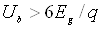 (6,6 В для Si). При високих концентраціях домішок (більше
1019 см–3) напруга лавинного пробою вища, чим тунельного,
і відбувається тунельний пробій, причому
(6,6 В для Si). При високих концентраціях домішок (більше
1019 см–3) напруга лавинного пробою вища, чим тунельного,
і відбувається тунельний пробій, причому 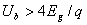 . Для проміжкових концентрацій
домішок (1018 см–3<Nдом<1019 см–3) пробій зумовлений обома механізмами. На практиці механізм пробою
визначають по знаку температурного коефіцієнта напруги пробою. Експериментально
встановлено також, що крутість ВАХ (
. Для проміжкових концентрацій
домішок (1018 см–3<Nдом<1019 см–3) пробій зумовлений обома механізмами. На практиці механізм пробою
визначають по знаку температурного коефіцієнта напруги пробою. Експериментально
встановлено також, що крутість ВАХ (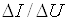 ) для лавинного пробою вища чим
для тунельного.
) для лавинного пробою вища чим
для тунельного.
Принципова електрична схема, яка використовується для досліджень,
представлена на рис. 7.2.
Завдання до лабораторної роботи
1. Зібрати електричну схему зображену на рис. 7.2.
2. Дослідити ВАХ низько- та високовольтних стабілітронів при трьох
температурах.
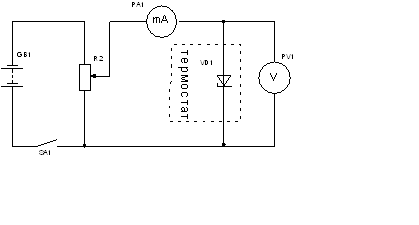
Рис. 7.2 Принципова електрична схема для дослідження Ub=f(T)
3. Побудувати графіки I=f(U). Визначити з цих
залежностей напругу пробою Ub – як початкову ділянку різкого зростання струму. По знаку 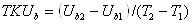 визначити
механізм пробою. Визначити крутість ВАХ
визначити
механізм пробою. Визначити крутість ВАХ 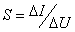 [mA/B] при однакових значеннях струму і порівняти
їх величини.
[mA/B] при однакових значеннях струму і порівняти
їх величини.
4. Для тунельного пробою за формулою (7.1) визначити концентрацію Nd при заданому Ек=1,4·106
В/см та ε=12 (Si). За
емпіричною формулою
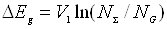 (7.3)
(7.3)
(V1=0,018 eB, NΣ=Nd+Na см–3,
NG=1017 см–3)
оцінити звуження ширини забороненої зони ΔЕg. Знайти значення концентрації неосновних носіїв заряду – р. Для
визначення р необхідно використати залежність
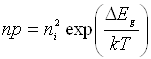 (7.4)
(7.4)
де ni –концентрація
носіїв заряду у власному напівпровіднику без врахування звуження ширини
забороненої зони (див. додаток 2).
У допущенні повної іонізації донорної домішки визначити положення рівня
Фермі (див. ф-лу (5.5)). Зобразити одержані результати на енергетичній
діаграмі.
5. Для випадку лавинного пробою за формулою (7.2) визначити ширину
забороненої зони Eg (N=Nd=2·1017 см–3). Розрахувати концентрацію неосновних носіїв заряду.
Визначити положення рівня Фермі. Представити одержані результати на
енергетичній діаграмі.
6. Порівняти отримані результати з літературними та довідниковими
даними. Зробити висновки.
Література
[1]. c. 248-278. [2]. c. 192-207. [4]. с. 270-273. [6]. с.
289-293.
Список рекомендованої літератури
1. Соболев В.Д. Физические основы
электронной техники. – М.: Высшая школа, 1979. – c. 248-278.
2. Герасимов С.М., Белоус М.В.,
Москалюк В.А. Физические основы электронной техники. – К.: Вища школа, 1981. – c. 192-207.
3. Кучерук І.М., Горбачук І.Т.
Загальна фізика: Підручник.–2-е вид., перероб. і допов. . – К.: Вища школа,
1995. – c. 151-166.
4. Шалимова К.В. Физика
полупроводников. М.: Энергия, 1976, – с. 270–273.
5. П.Т. Орешкин Физика полупроводников и диэлектриков. – М:,
Высшая школа, 1977. с. 191-210.
6. Г.И.
Епифанов. Физические основы микроэлектроники. М.: Советское радио, 1971, –
с.320.
Додаток 1
Врахування спектрального розподілу
густини випромінювання лампи розжарювання
Кількість енергії, яка випромінюється за одиницю часу з одиниці площі в
одиничному інтервалі частоти абсолютно чорним тілом в одиничному інтервалі
частоти 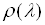 може
бути знайдена за формулою Планка:
може
бути знайдена за формулою Планка:
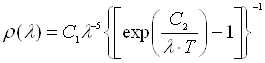 (Д.1)
(Д.1)
де С1 і С2 – постійні (С1=3,74·10–16
Вт·м2; С2=1,438·10–2 м·К).
Якщо в якості джерела світла використовується лампа розжарювання з
вольфрамовою спіраллю, то необхідно врахувати коефіцієнт чорноти для вольфраму.
Відомо, що при температурі 1600 К цей коефіцієнт лінійно зменшується від 0,5 (λ=0,4 мкм) до 0,32 (λ=1,2 мкм), а при температурі 2800 К від
0,42 до 0,32 для вказаних довжин хвиль.
Для зручності користування формулу Планка записують у приведеному
вигляді через безрозмірні величини X та Y:
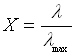 ;
;
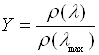 (Д.2)
(Д.2)
де 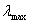 –
значення довжини хвилі, яка відповідає максимуму випромінювання при T=const.
–
значення довжини хвилі, яка відповідає максимуму випромінювання при T=const. 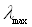 знаходиться за законом
Віна:
знаходиться за законом
Віна:
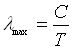 , С=2898
мкм·К. (Д.3)
, С=2898
мкм·К. (Д.3)
З врахуванням (Д.2) формулу Планка можемо записати у зручному для
розрахунків вигляді:
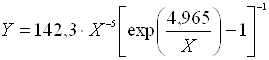 .
(Д.4)
.
(Д.4)
При приведенні результатів дослідження спектральної залежності величини
фотоструму до одиниці поглинутої енергії необхідно 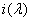 ділити на відповідні значення Y з врахуванням коефіцієнта чорноти. Якщо
необхідно провести нормування до одиниці поглинутих фотонів, то необхідно
отриману величину розділити на енергію кванта
ділити на відповідні значення Y з врахуванням коефіцієнта чорноти. Якщо
необхідно провести нормування до одиниці поглинутих фотонів, то необхідно
отриману величину розділити на енергію кванта 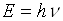 . Енергію кванта зручно знаходити
за формулою:
. Енергію кванта зручно знаходити
за формулою:
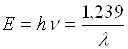 ,
де
,
де 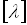 – мкм.
– мкм.
Література
1. Г.Г.
Ишанин, Э.Д. Панков, В.С. Радайкин. Источники и приемники излучения. – М.:
Машиностроение, 1982, 222 с.
2. Л.З.
Криксунов. Справочник по основам инфракрасной техники. – М.: Советское радио,
1978, – 400 с.
Додаток 2
Властивості власних напівпровідників Si, Ge і GaAs при 300 К
|
|
Si |
Ge |
GaAs |
|
Ширина забороненої зони Еg, еВ
|
1,1 |
0,66 |
1,43 |
|
Ефективна густина станів,
см–3:
NC
NV
|
2,8·1019
1,02·1019
|
1,04·1019
6,1·1018
|
4,4·1017
8,6·1018
|
|
Власна концентрація, ni, см–3
|
1,45·1010
|
2,4·1013
|
1,3·107
|
|
Дрейфова рухливість
електронів і дірок, см2/(В·с)
μn
μp
|
1350
480
|
3900
1900
|
8500
400
|
|
Дрейфова швидкість
насичення електронів і дірок, см/с
vsn
vsp
|
1·107
8·106
|
6·106
6·106
|
1·107
–
|
| Питомий опір ρ, Ом·см |
2,3·105
|
47 |
5·106
|
| Відносна діелектрична
проникність ε |
12 |
16 |
11 |
|
Електричне поле пробою Екр,
кВ/см
|
300 |
100 |
400 |
| Коефіцієнт теплопровідності
λ, Вт/(см·К) |
1,45 |
0,64 |
0,46 |
| Питома теплоємність С,
Дж/(г·К)) |
0,7 |
0,31 |
0,35 |